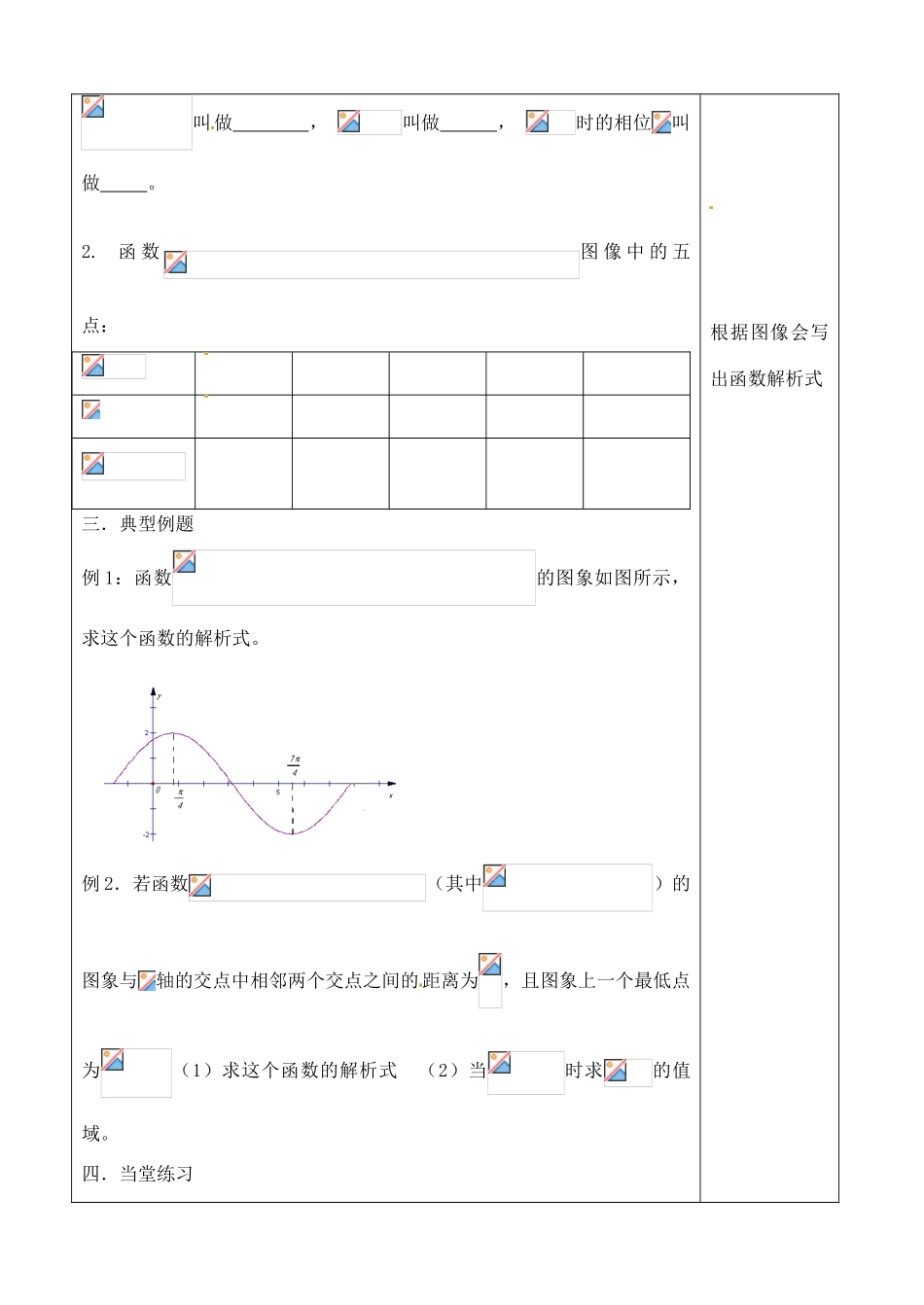
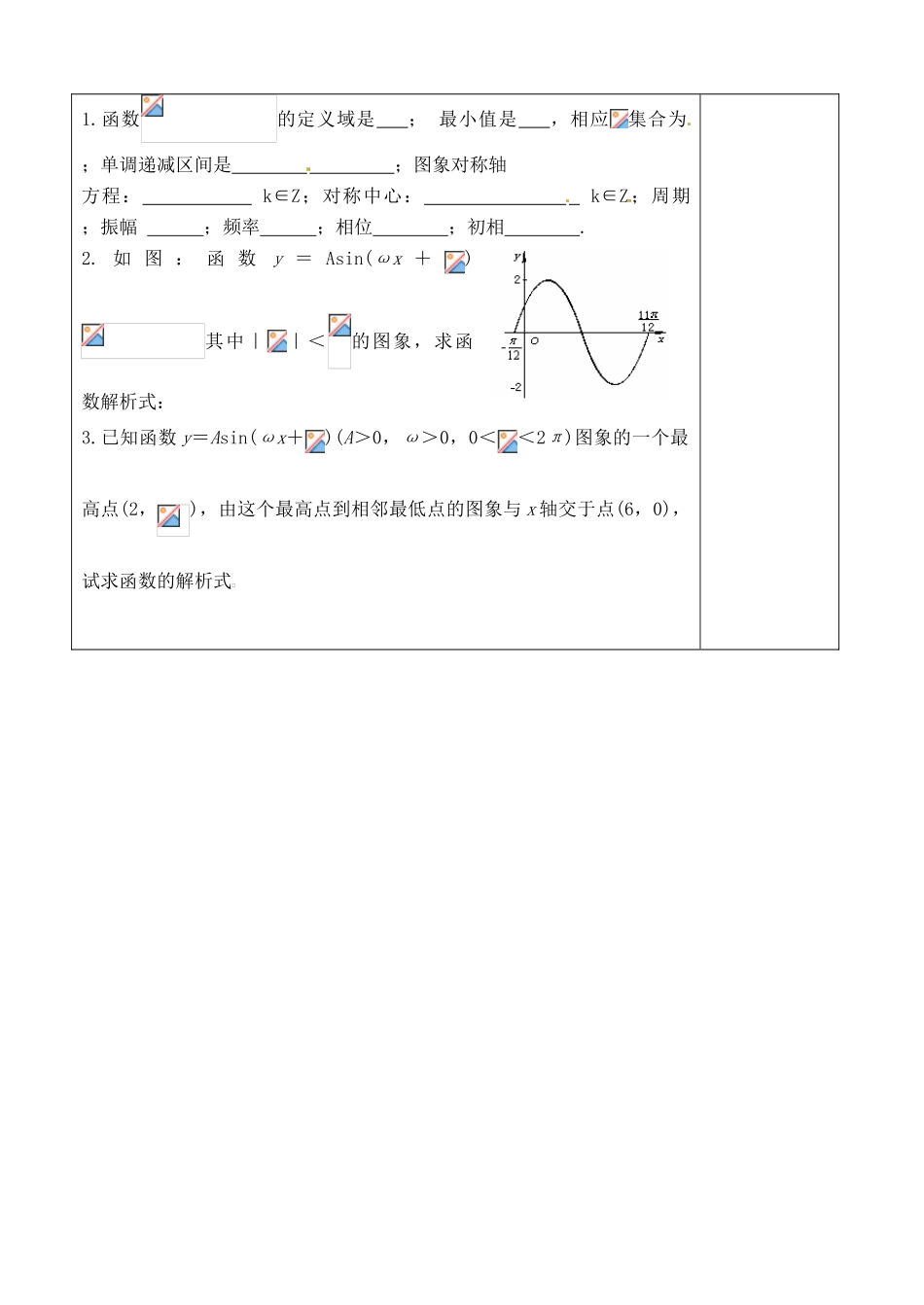
吉林省吉林市朝鲜族中学 2014 高中数学 1.5.2 函数 y=Asin(ax+b)图像与性质学案(无答案)新人教 A 版必修 4学习目标1.理解振幅、周期、频率、相位和初相与 A, ω ,φ 的关系。2.根据三角函数的图象给出的条件求函数解析式.学习重点根据三角函数的图象给出的条件会求函数解析式.学习难点根据三角函数的图象给出的条件会求函数解析式. 学 习 内 容学法指导一.复习(1)的图象如何变换可得到的图象?(2)的图象如何变换可得到的图象?(3)向左平移,横坐标伸长为原来的二倍,求所得函数解析式?(4)可由如何变换得到?方法一:方法二:二.知识点:1.函数中:A 表示一个振动量时,A 叫做 ,叫做 ,自主练习掌 握叫做 , 叫做 , 时的相位叫做 。2. 函 数图 像 中 的 五点:三.典型例题例 1:函数的图象如图所示,求这个函数的解析式。例 2.若函数(其中)的图象与轴的交点中相邻两个交点之间的 距离为,且图象上一个最低点为(1)求这个函数的解析式 (2)当时求的值域。四.当堂练习根据图像会写出函数解析式1.函数的定义域是 ; 最小值是 ,相应集合为 ;单调递减区间是 ;图象对称轴方程: k∈Z;对称中心: k∈Z;周期 ;振幅 ;频率 ;相位 ;初相 .2. 如 图 : 函 数y = Asin(ωx +)其中||<的图象,求函数解析式:3.已知函数 y=Asin(ωx+)(A>0,ω>0,0<<2π)图象的一个最高点(2,),由这个最高点到相邻最低点的图象与 x 轴交于点(6,0),试求函数的解析式