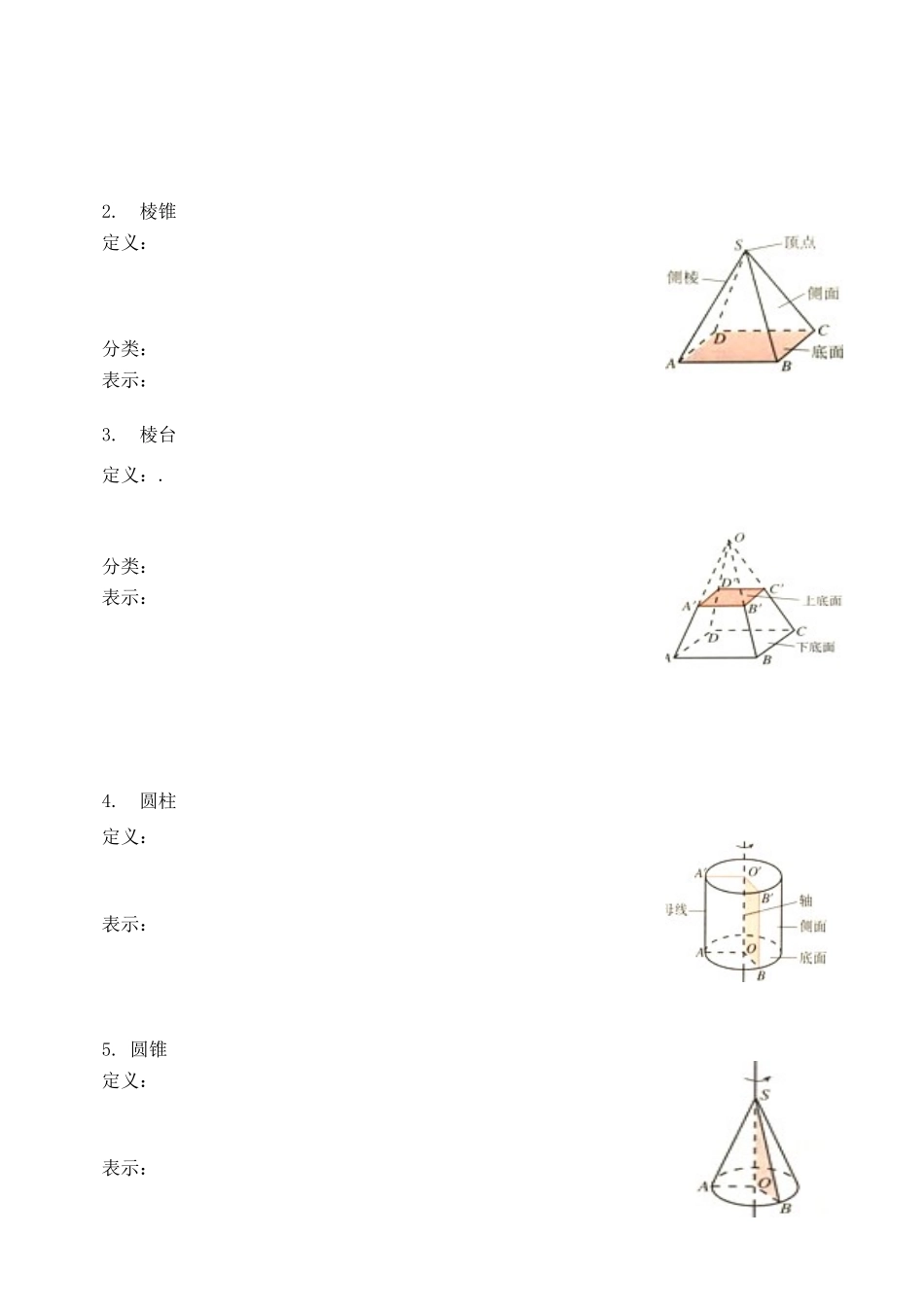
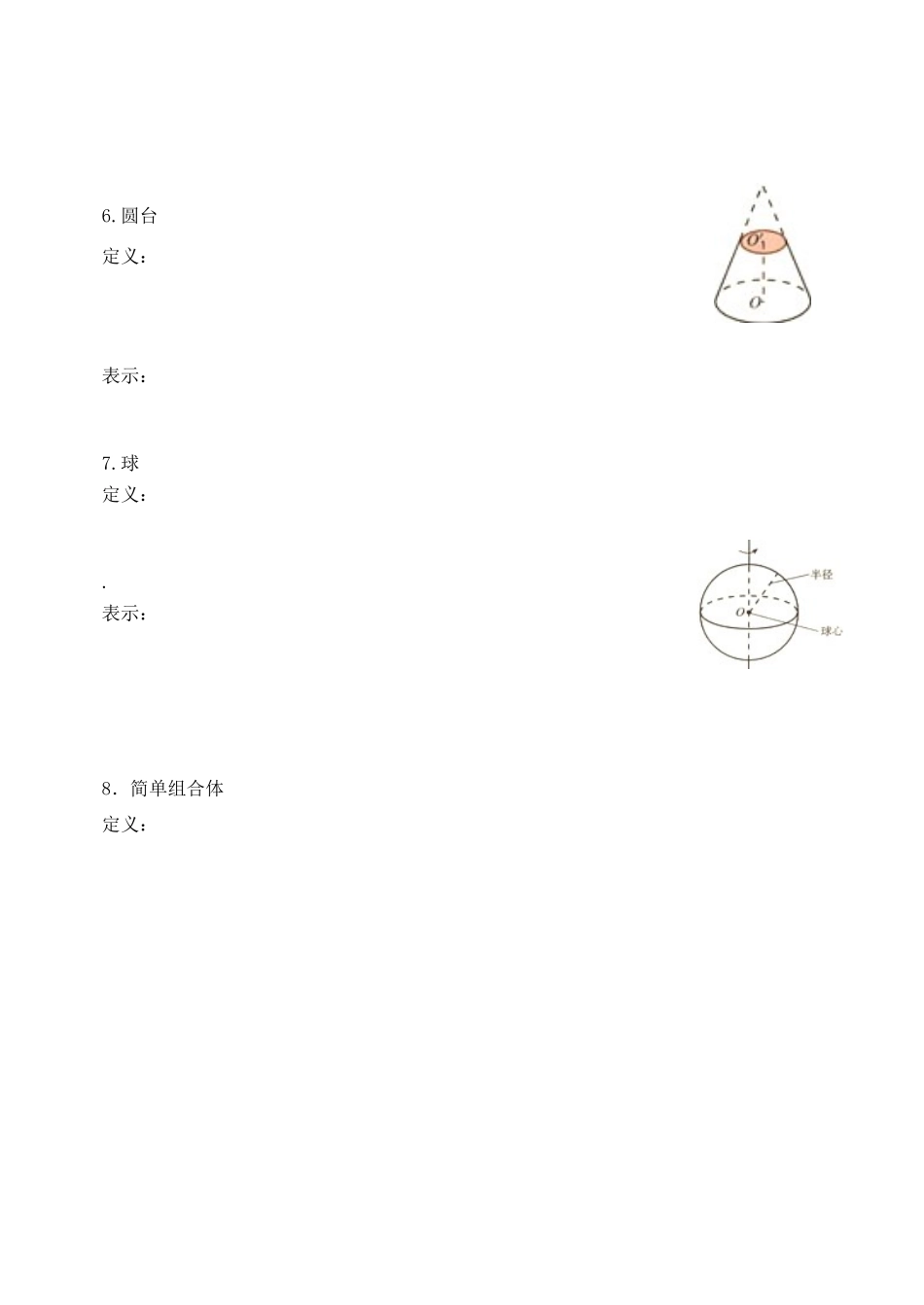
第一章 空间几何体【高考要求】① 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.② 知道平行投影与中心投影的概念,了解空间图形的不同表示形式. ③ 能画出简单空间图形(长方体、棱柱、圆柱、圆锥、球等及其简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图.④ 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).1.1 空间几何体的结构(1,2 课时)【学习目标】 感受大量空间实物及模型,概括出柱、锥、台、球的结构特征。【教学重难点】 柱、锥、台、球的结构特征的概括。【课前导学】阅读教材第 2—8 页,完成下列学习一、多面体与旋转体1.多面体: 叫做多面体,其中 叫做多面体的面, 叫做多面体的楞, 叫做多面体的顶点。2.旋转体: 叫做旋转体, 其中 叫做旋转体的轴。二、柱、锥、台、球的结构特征1.棱柱定义:分类:表示: 2.棱锥定义:分类: 表示:3.棱台定义:.分类: 表示: 4.圆柱定义:表示:5. 圆锥定义:表示: 6.圆台定义:表示: 7.球定义:.表示: 8.简单组合体定义:【预习自测】1.下列命题中正确的是( )A.由五个平面围成的多面体一定是四棱锥B.棱锥的高线可能在几何体之外C.仅有一组对面平行的六面体是棱台D.有一个面是多边形,其余各面是三角形的几何体是棱锥2. 下列命题中正确的是( )A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台3.直角三角形绕其一边旋转一周所形成的几何体是否是圆锥?【典型例题】例 1.判断下图中所示物体是不是棱台,为什么?(其中面与面 ABCD,在图(1)中平行,在图(2)中不平行)例 2. 如图,已知长方体 ABCD-A1B1C1D1,过 BC 和 AD分别作一个平面交底面 A1B1C1D1于 EF、PQ,则长方体被分成三个几何体中,棱柱的个数是 例 3.把一个圆锥截成圆台,已知圆台的上、下底半径的比是 1︰4,圆台的母线长是9cm,求圆锥的母线长.