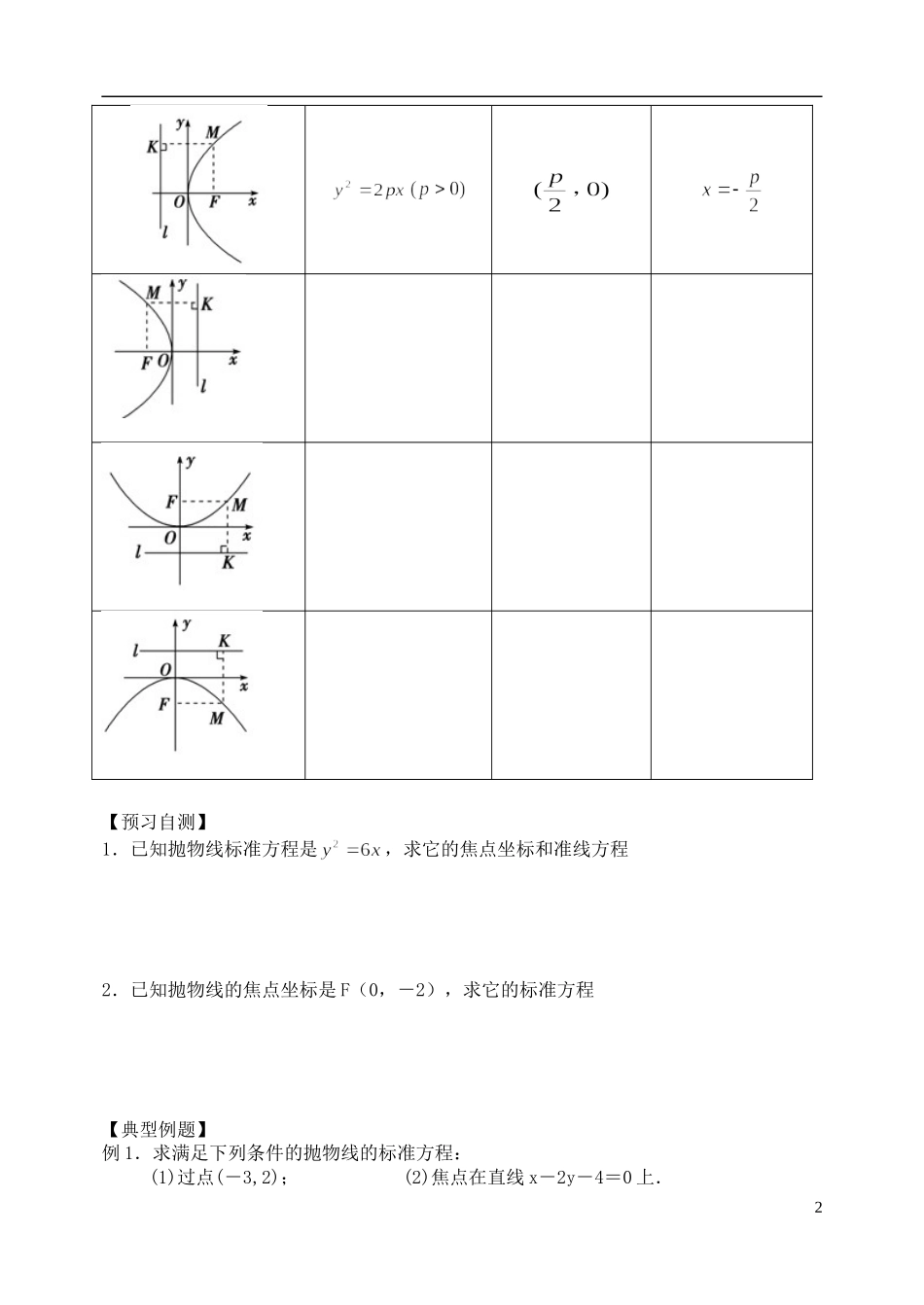
2.4 抛物线(4 课时)2.4.1 抛物线及其标准方程(第 1 课时)【教学目标】1.使学生掌握抛物线的定义,标准方程及其推导过程;2.根据定义画出抛物线的草图 3.使学生能熟练地运用坐标,进一步提高学生“应用数学”的水平 【教学重点】抛物线的定义【教学难点】抛物线标准方程的不同形式【课前导学】阅读教材完成下列学习一. 抛物线定义:__________________________________________________叫做抛物线定点 F 叫做抛物线的______,定直线 叫做抛物线的______ 二.抛物线的标准方程:推导:方程__________________________叫做抛物线的标准方程相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的,即 不同点:(1)图形关于 X 轴对称时,X 为一次项,Y 为二次项,方程右端为、左端为;图形关于 Y 轴对称时,X 为二次项,Y 为一次项,方程右端为,左端为 (2)开口方向在 X 轴(或 Y 轴)正向时,焦点在 X 轴(或 Y 轴)的正半轴上,方程右端取正号;开口在 X 轴(或 Y 轴)负向时,焦点在 X 轴(或 Y 轴)负半轴时,方程右端取负号 抛物线标准方程的四种形式图形标准方程焦点坐标准线方程1【预习自测】1.已知抛物线标准方程是,求它的焦点坐标和准线方程 2.已知抛物线的焦点坐标是 F(0,-2),求它的标准方程【典型例题】例 1.求满足下列条件的抛物线的标准方程:(1)过点(-3,2); (2)焦点在直线 x-2y-4=0 上.2例 2.(1)已知点 P 是抛物线 y2=2x 上的一个动点,求点 P 到点(0,2)的距离与 P 到该抛物线准线的距离之和的最小值.(2)已知点 P 是焦点为 F 的抛物线 y2=2x 上的一个动点,点 A(3,2),求|PA|+|PF|的最小值.例 3.喷灌的喷头装在直立管柱 OA 的顶部 A 处,喷出的水流的最高点为 B,距地面 5m,且与管柱 OA 相距 4m,水流落在以 O 为圆心,半径为 9m 的圆上,求管柱 OA 的长.3