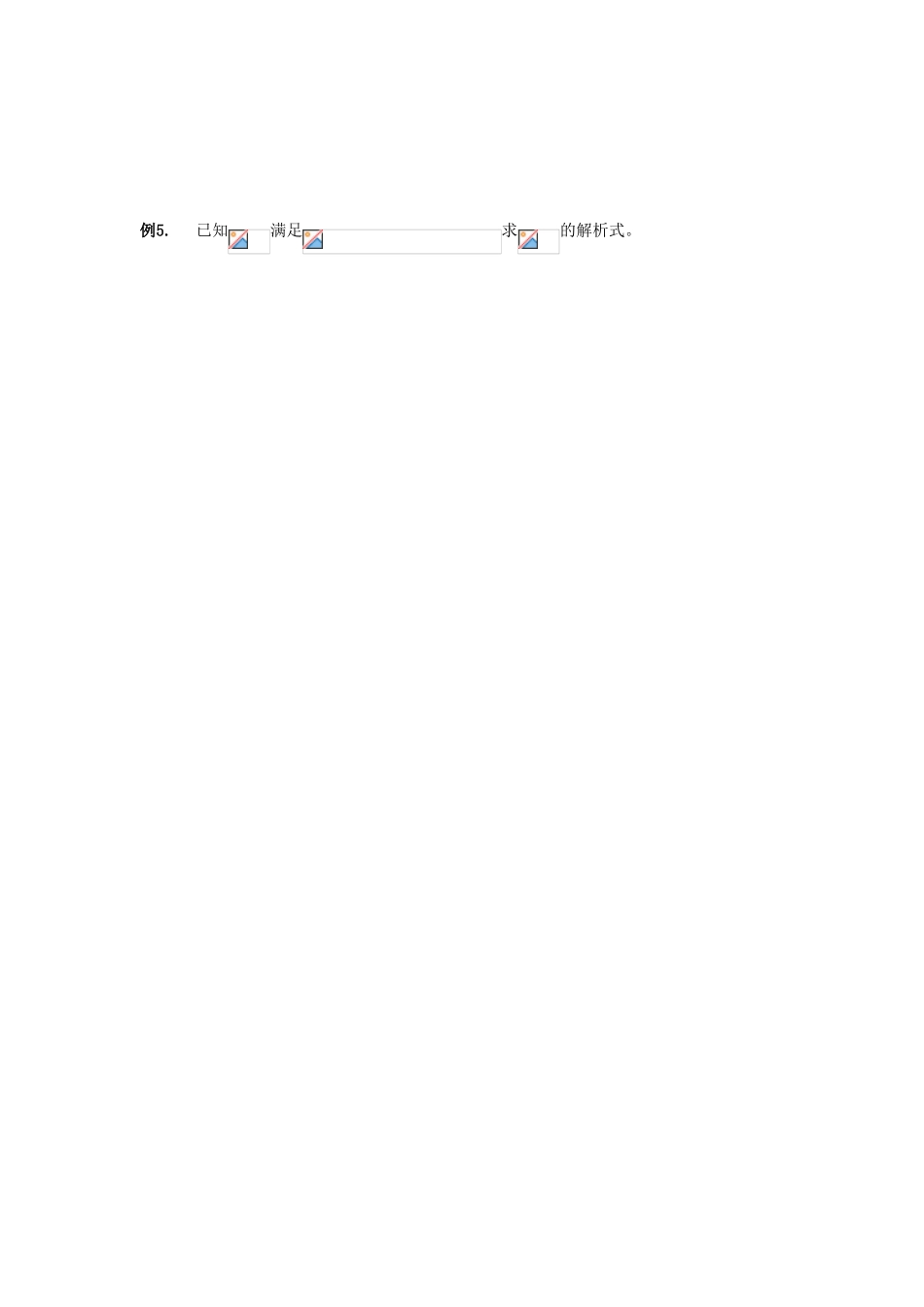
第四课时 1.2.2 函数的表示法(1)学习目标1. 明确函数的三种 表示方法(解析法、列表法、图象法),了解三 种表示方法各自的优点,在实际情境中,会根据不同的需要选择恰当的方法表示函数;2. 通过具体实例,了解简单的分段函数,并能简单应用.3. 了解映射的概念及表示方法;结合简单的对应图示,了解一一映射的概念;4. 理解函数的概念及三种表示分方法会求函数解析式;5. 能熟练地画出函数的图像,领悟学 习数形结合思想的重要性.重点 1. 通过具体实例,了解简单的分段函数,并能简单应用.2. 理解函数的概念及三种表示分方法会求函数解析式难点 能熟练地画出函数的图像,领悟学习数形结合思想的重要性【课前导学】阅读教材第 19-22 页,完成新知学习1. 函数的表示法常用的有__________、__________、__________。解析法:用 表示两个变量之间的对应关系. 优点:简明;给自变量求函数值图象法:用 表示两个变量之间的对应关系. 优点:直观形象,反应变化趋势.列表法: 来表示两个变量之间的对应关系. 优点:不需计算就可看出函数值. 2.分段函数:在函数的定义域内,对于自变量的不同取值区间,有着 ,这样的函数通常叫 做 。关键:“分段函数,分段处理”3.映射:一般地,设 A、B 是两个 的 ,如果按某一个确定的对应法则 f,使对于集合 A 中的 x,在集合 B 中都有 的元素 y 与之对应,那么就称对应为从集合 A 到集合 B 的一个 .记作“” 关键:A 中任意,B 中唯一;对应法则 f.4.函数与映射的关系:函数是建立在两个非空数集间的一种对应,若将其中的条件“ ”弱化为“任意两个非空集合”,按照某种法则可以建立起更为普通的元素之间的对应关系,即映射. 简言之:函数一定是映射,而映射不一定是函数.5.对于映射:A→B,我们把集合中的元素叫原象,中与原象对应的元素叫做象。【预习自测】首先完成教材上 P23 第 1、2 题;然后做自测题1.已知,则。2.已知,则= ;= .3.下列对应是否是集合 A 到集合 B 的映射?(1),对应法则是“乘以 2”;(2)A= R*,B=R,对应法则是“求算术平方根”;(3)R,对应法则是“求倒数”.【典型例题】例1.已知求的解析式。例2.已知求的解析式。例3.已知为二次函数,且求例4.已知满足求的解析式。例5.已知满足求的解析式。