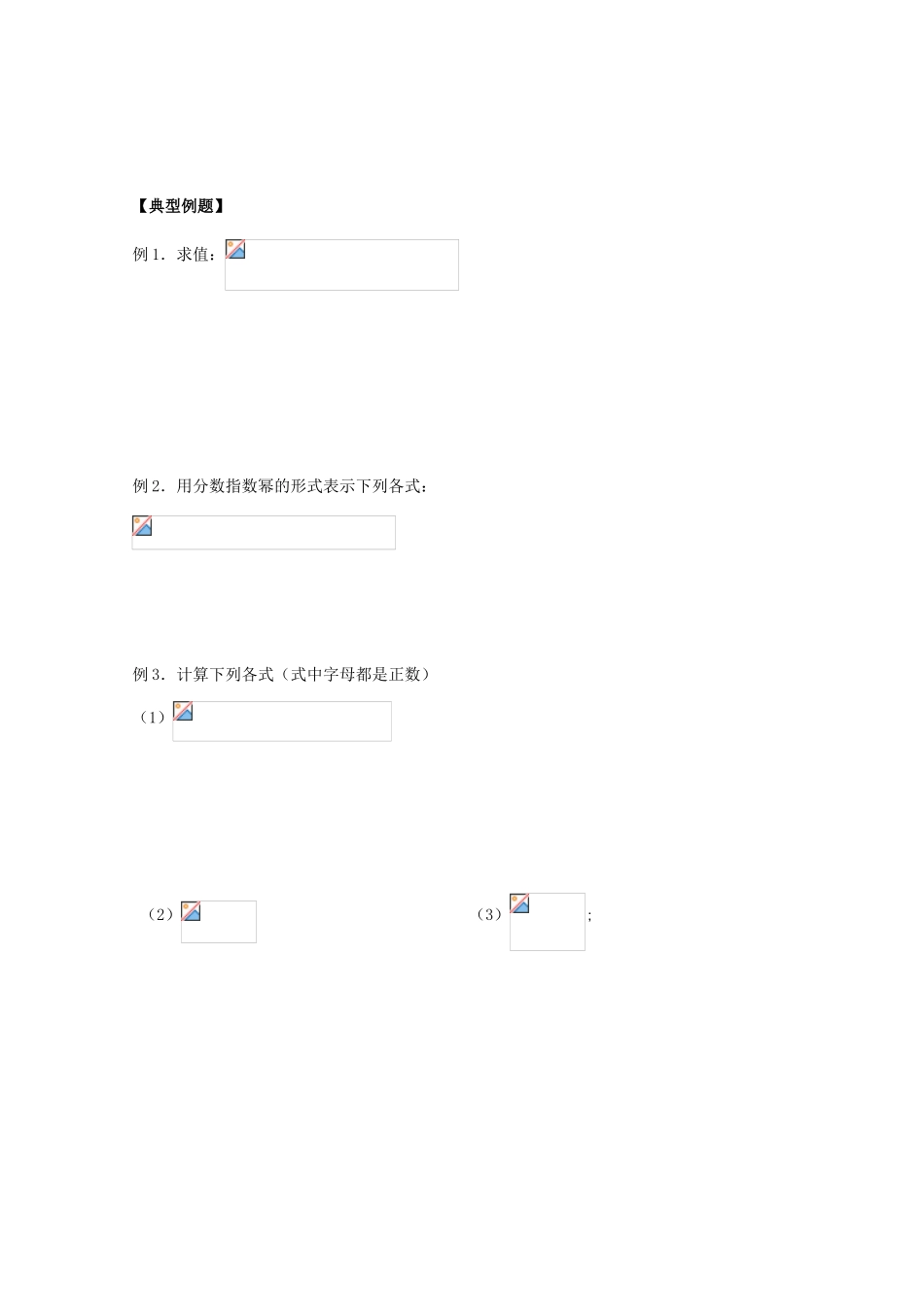
第一课时 2.1.1 指数与指数幂的运算(1)考纲要求:(1)掌握根式的概念和性质,并能熟练应用于相关计算中 (2)理解分数指数幂的概念,掌握有理指数幂的运算性质,会对根式、分数指数幂进行互化. (3)理解指数函数的概念,并能正确作出其图象,掌握指数函数的性质.(4)掌握指数形式的函数定义域、值域,判断其单调性. 学习目标1、理解指数幂指数取值范围的扩充,能够进行分数指数幂与根式的互化2、掌握有理数指数幂的运算性质,灵活地运用运算公式进行有理数指数幂的运算和化简,会进行根式与有理数指数幂的相互转化。重点、难点 掌握有理数指数幂的运算性质,灵活地运用运算公式进行有理数指数幂的运算和化简,会进行根式与有理数指数幂的相互转化。【课前导学】1、 根式:(1) 次方根的定义 _____________________________________ (2)的次方根的取值规律: ① 当为奇数时,的 次方根为一个正数;,的次方根为一个负数; ,的次方根为零. ② 当 为偶数时,a 的次方根为两个互为相反数的数;,a 的次方根不存在; ,a 的次方根为零.(3) 的次方根的符号表示___________________________ (4)根式运算的依据2、 分数指数幂(1).分数指数幂正数的分数指数幂的意义,规定:,0 的正分数指数幂等于 0,0 的负分数指数幂没有意义(2).实数指数幂的运算性质(1)(2)(3)【预习自测】1、化简① . ② .③.(<)2、求下列各式的值:(1); (2); (3)【典型例题】例 1.求值:例 2.用分数指数幂的形式表示下列各式:例 3.计算下列各式(式中字母都是正数)(1) (2) (3);