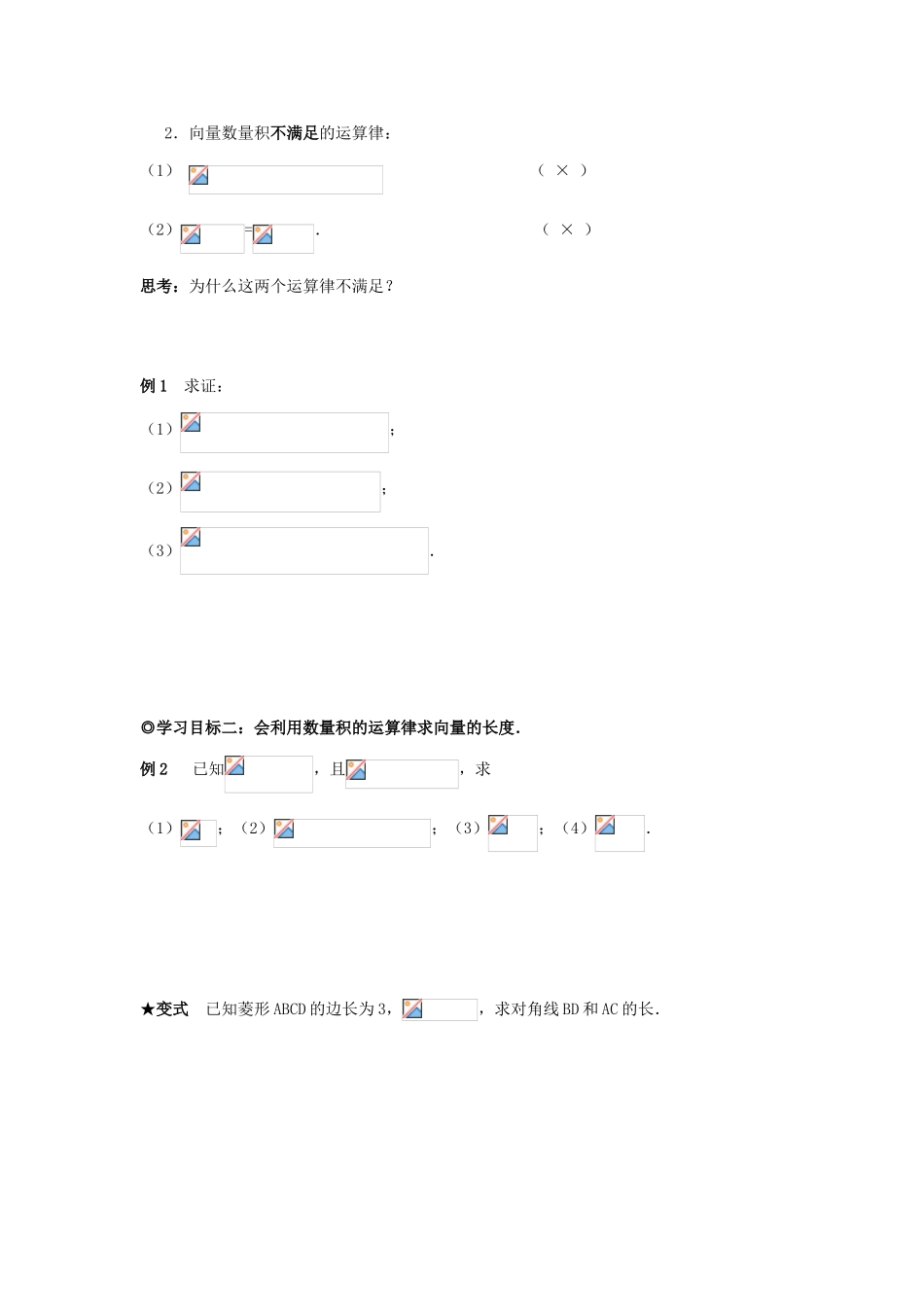
§2.3.2 向量数量积的运算律◆ 课前导学(一)学习目标1.记住向量数量积满足的运算律和不满足的运算律;2.会利用数量积的运算律求向量的长度;3.会利用数量积的运算律解决几何问题.(二)重点难点重点:记住向量数量积满足的运算律和不满足的运算律,会利用数量积的运算律求向量的长度;难点:会利用数量积的运算律解决几何问题.(三)温故知新1. 向量的长度公式:____________________________________,向量的距离公式::____________________________________,向量的夹角公式::____________________________________;2.实数乘法的运算律:(1)交换律:______;(2)结合律:______;(3)分配律:_____________________.3.数量积的运算结果是一个____________,数与向量的乘积结果是一个____________.◆ 课中导学◎学习目标一:记住向量数量积满足的运算律和不满足的运算律.(一) 概念形成1. 向量数量积满足的运算律:(1)交换律:______;(2)数乘结合律:=____________=____________;(3)分配律:_____________________.2.向量数量积不满足的运算律:(1) ( × )(2)=. ( × )思考:为什么这两个运算律不满足?例 1 求证:(1);(2);(3).◎学习目标二:会利用数量积的运算律求向量的长度.例 2 已知,且,求(1);(2);(3);(4).★变式 已知菱形 ABCD 的边长为 3,,求对角线 BD 和 AC 的长.◎学习目标三:会利用数量积的运算律解决几何问题.例 3 求证:菱形的两条对角线互相垂直.★变式 1 求证:平行四边形两条对角线平方和等于四条边的平方和.★变式 2 若,,已知,则与的关系如何?★变式 3 在中,若,那么点 A 在的什么位置? ◆ 课后导学一、选择题1.如果,且,那么( )A. B. C. D.在方向上的投影相等2.下列各式中正确命题的个数为( )(1);(2);(3); (4).A.1 B.2 C.3 D.43.下列各命题(1)若,则对任一向量,得;(2)若,则对任一向量,得;(3)若,,则;(4)若,则中至少有一个为;(5)若,,则;(6)若,则,当且仅当时成立.其中真命题的个数为( )A.1 B.2 C.3 D.44.若,,且,则以下表述错误的是( )A. B. C. D.以为邻边的平行四边形是矩形 5.若,则为( )A.钝角三角形 B.锐角三角形 C.等腰直角三角形 D.直角三角形6.在中,若,则点 O 是的( )A.内心 B.外心 ...