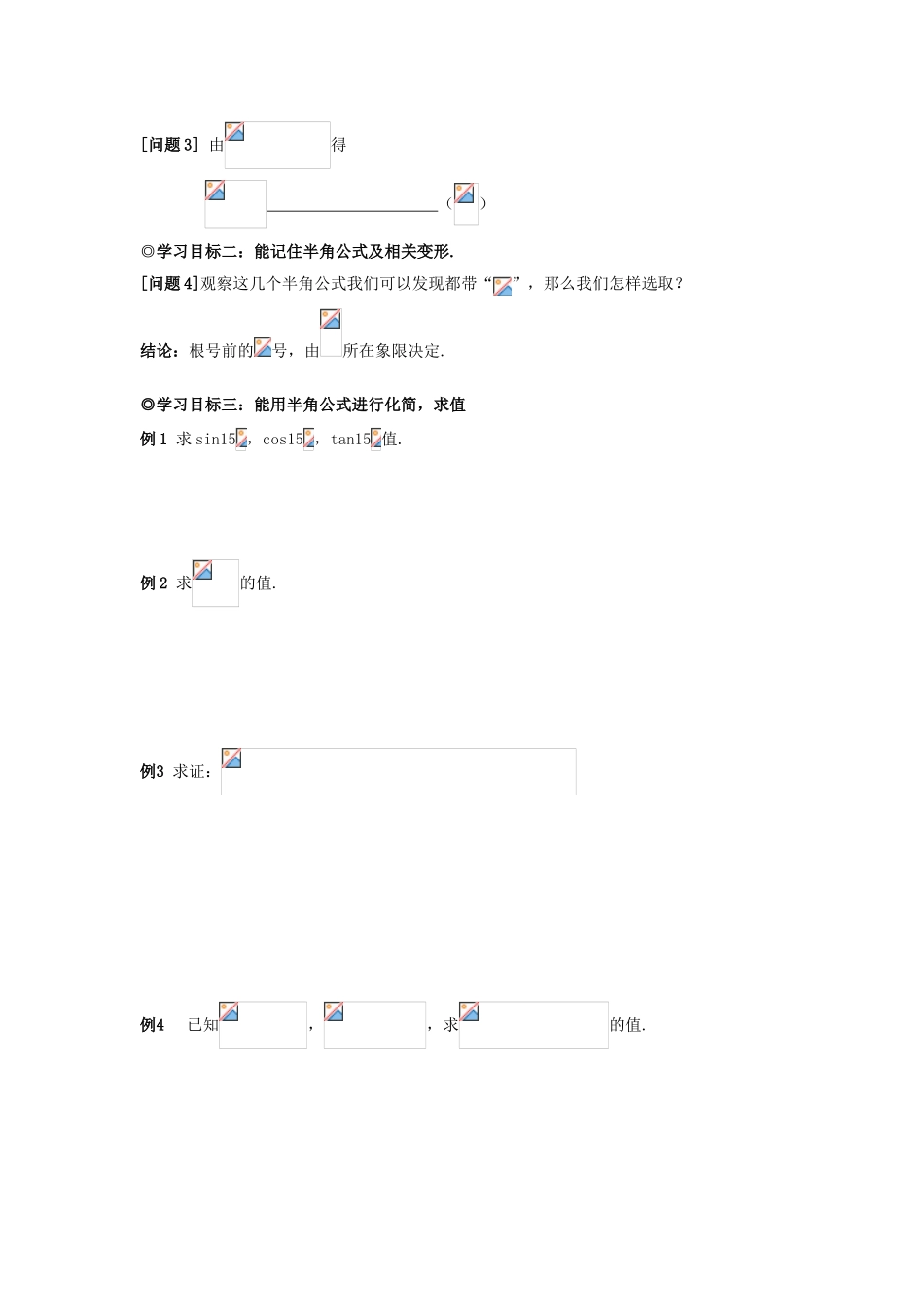
§3.2.2 半角公式◆ 课前导学(一) 学习目标1.学会利用二倍角公式,推导出半角的正弦、余弦和正切公式,知道各公式之间的内在联系,认识整个公式体系的生成过程;2. 能记住半角公式及相关变形;3. 能用半角公式进行化简,求值.(二)重点难点重点:掌握半角的正弦、余弦、正切公式的结构特点,灵活用公式;方程思想,分类讨论思想,和化归思想的运用; 难点:公式前符号的确定;变换中三统一原则的运用; “倍与半”的相对性思考方法.半角与倍角公式之间的内在联系. (三)温故知新余弦的倍角公式=____________=______________=________________________,___________◆ 课中导学◎学习目标一:学会利用二倍角公式,推导出半角的正弦、余弦和正切公式,知道各公式之间的内在联系,认识整个公式体系的生成过程 [问题 1] 有什么关系?用可表示为______________________;[问题 2] 怎么用来表示 cos、sin? 即 cos= () sin= ()[问题 3] 由得 () ◎学习目标二:能记住半角公式及相关变形.[问题 4]观察这几个半角公式我们可以发现都带“”,那么我们怎样选取?结论:根号前的号,由所在象限决定.◎学习目标三:能用半角公式进行化简,求值例 1 求 sin15 ,cos15 ,tan15 值.例 2 求的值.例3 求证: 例4已知,,求的值.例5已知,是第四象限角,求.★变式 已知,求(1);(2);(3).例6化简◆课后导学一、选择题1. , 则的值等于 ( )A、 B、 C、 D、2、设 则 ( )A、 B、 C、 D、3、若 ( )A、 最小正周期为 B、最小正周期为的奇函数C、最小正周期 D、最小正周期为的偶函数4. 已知 sin=,那么的值为( )A.-3 B.3 C.- D. 5.设 A.sin B.cos C. -sin D. -cos6. 已知 cos()cos()=,则等于( )A. B. C. D. 7. 化简()-()的结果为( )A. B.2 C.2sin D. 2cot二、解答题8. 求下列函数的周期(1) (2)9. 已知,并且,求的值10.等腰三角形的顶角的余弦等于,求这个三角形一个底角的正弦和余弦.11.已知 , 设① 求函数的最小正周期② 当