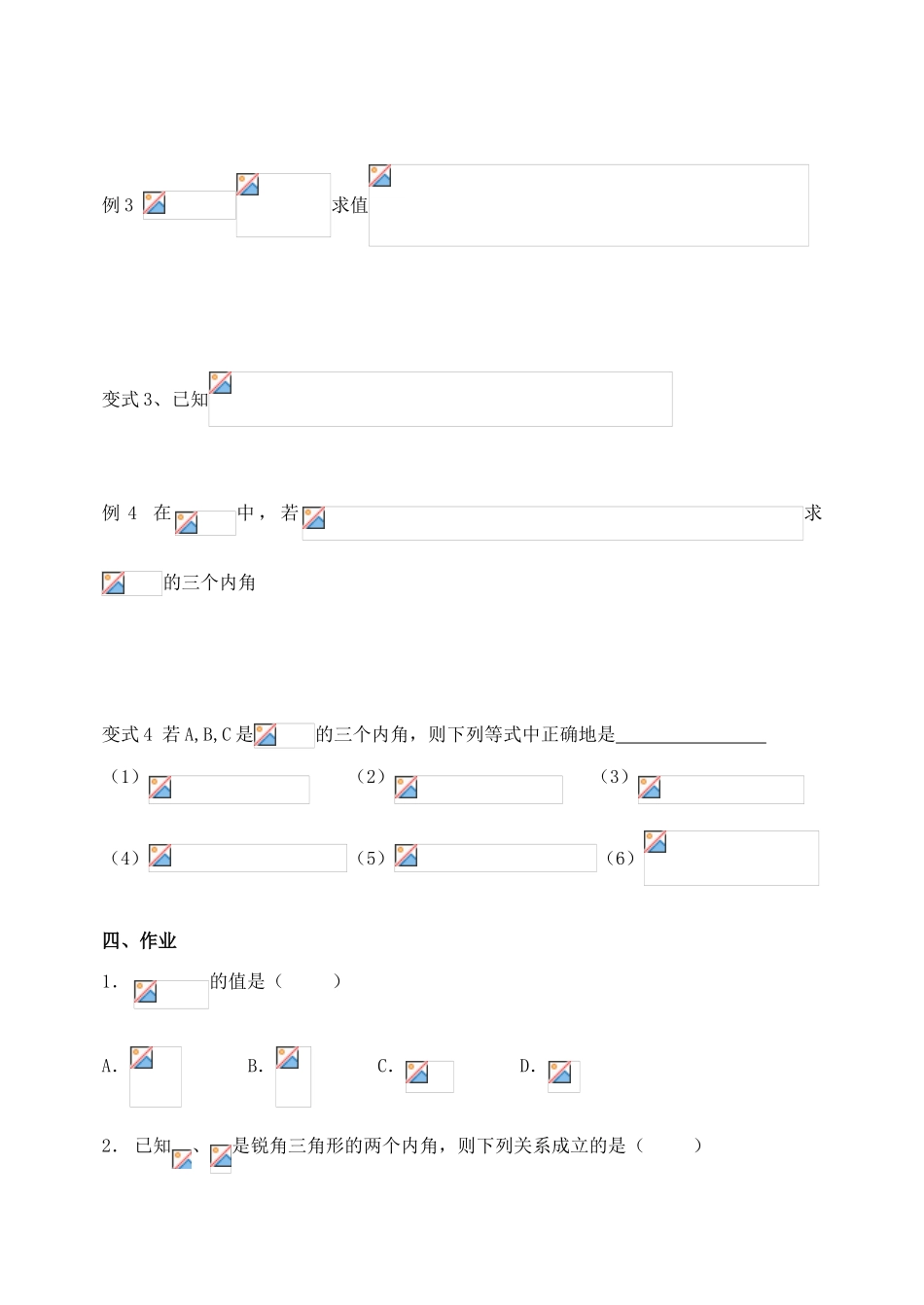
山东省聊城四中 2014 届高考数学一轮复习 3.2 同角三角函数基本关系及诱导公式学案一、高考目标:1、理解同角三角函数的基本关系2、能利用单位圆中的三角函数线推出的正弦、余弦、正切诱导公式二、知识梳理1、 同角三角函 数的基本关系(1)平方关系: (2)商数关系 注:“同角”的概念与表达形式无关;有一个角的任一三角函数值可求另两个三角函数值。2、 三角函数的对称关系(1)终边与角的终边关于 对称的角可表示为(2)终边与角的终边关于轴对称的角可表示为 s (3)终边与角的终边关于 对称的角可表示为(4)边与角的终边关于直线对称的角可表示为 3、 三角函数的诱导公式(1)公式一 (2)公式二 (3)公式三 (4)公式四 (5)公式五 (6)公式六 4、 任意角的三角函数化为锐角三角函数的步骤 ( ) ( )任意角的三角函数 任意正角的三角函数 ( )0 到的三角 函数 锐角三角函数。三、考点例析例 1 已知的值变式 2:化简例 3 求值变式 3、已知例 4 在中 , 若求的三个内角变式 4 若 A,B,C 是的三个内角,则下列等式中正确地是 (1) (2) (3)(4)(5)(6)四、作业1.的值是( )A. B. C. D.2. 已知、是锐角三角形的两个内角,则下列关系成立的是( )① ② ③ ④A.①③ B.①④ C.②③ D.②④3. 已知,则的值是( )A. B. C. D.4. 已知满足,则( )A. B. C. D. 5.如果的三个内角的余弦值分别等于的三个内角的正弦值,则( )A.和都是锐角三角形 B.和都是钝角三角形C.是钝角三角形,是锐角三角形D.是锐角三角形,是钝角三角形6.已知,则( )A. B. C. D.7.= .8..若,则= .9.设,求= 10.如果,且是第四象限角,那么= .11.已知=