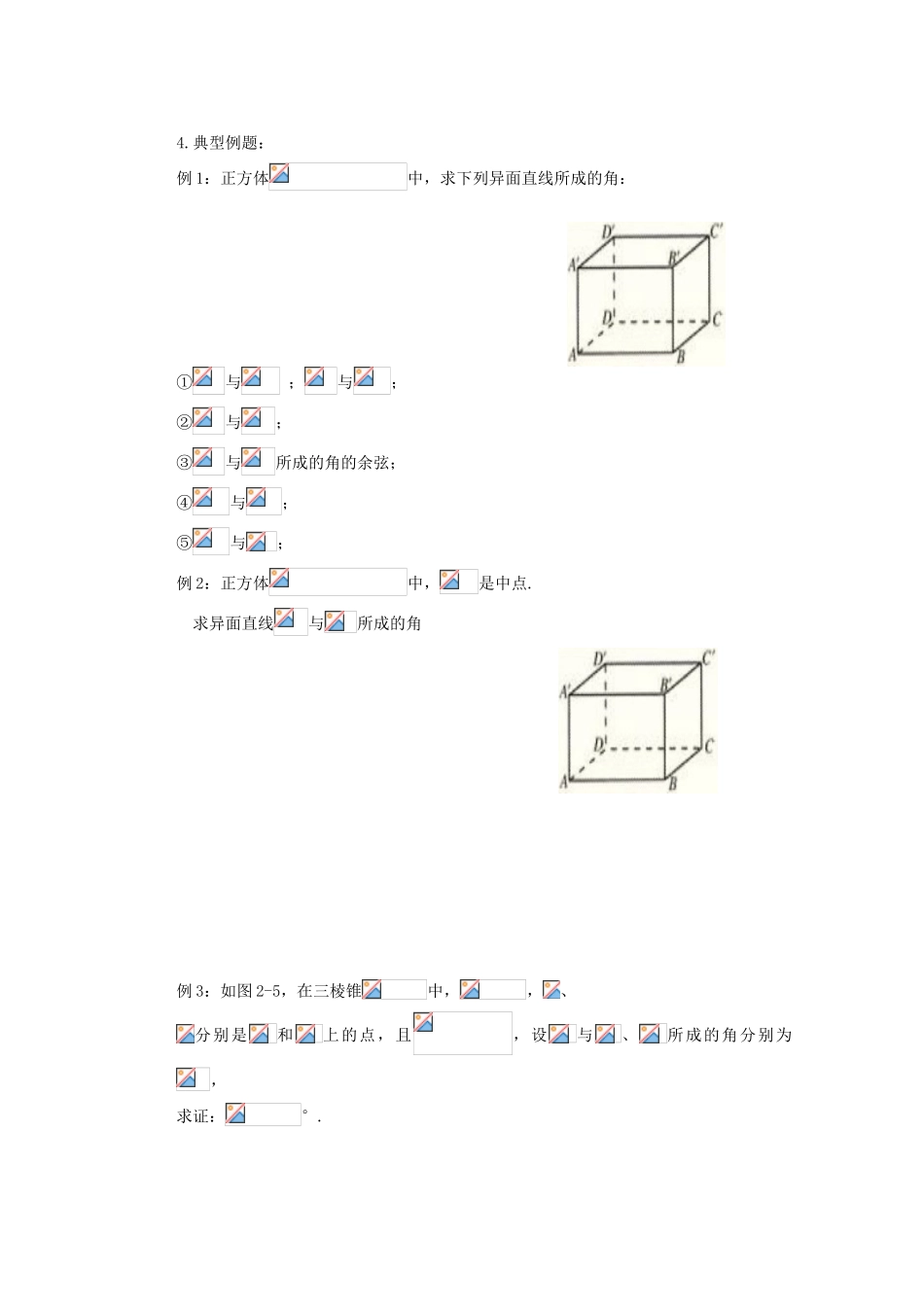
山西省朔州市平鲁区李林中学高中数学 小结与复习 异面直线所成的角导学案 新人教 A 版必修 2二、课堂识真:1.复习回顾:复习 1:空间任意两条直线的位置关系有_______、___ ___、_______三种.复习 2:异面直线是指________________________复习 3:平行公理:________________________________;空间等角定理:__________________________________________.2.导入新课:问题:平面内两条直线的夹角是如何定义的?想一想两条异面直线的相对倾斜程度如何描述?3.异面直线所成的角:⑴ 定义:问题:①作异面直线夹角时,夹角的大小与点的位置有关吗?点的位置怎样取才比较简便?② 异面直线所成的角的范围是多少?③ 两条互相垂直的直线一定在同一平面上吗?④ 异面直线的夹角是通过什么样的方法作出来的?它体现了什么样的数学思想?⑵ 异面直线所成角的方法------平行平移法⑶ 求异面直线所成角的步骤:作---证---求.4.典型例题:例 1:正方体中,求下列异面直线所成的角: ①与 ;与;②与;③与所成的角的余弦;④与;⑤与;例 2:正方体中,是中点. 求异面直线与所成的角 例 3:如图 2-5,在三棱锥中,,、分别是和上的点,且,设与、所成的角分别为,求证:°.三、课后见功:1.如图 4-4,是正方体的平面展开图,图 4-4则在这个正方体中:①与平行 ②与是异面直线③与成 60°角 ④与是异面直线其中正确命题的序号是( )A.①②③ B.②④ C.③④ D.②③④ 2.空间四边形,是与中点,,求与所成的角.3.如图,正三棱柱中(底面为正三角形,侧棱垂直于底面)中,若,求与所成的角.四、拾遗补缺:求异面直线所成的角的方法:① 直接平移法;② 中位线平移法;③ 补形平移法.