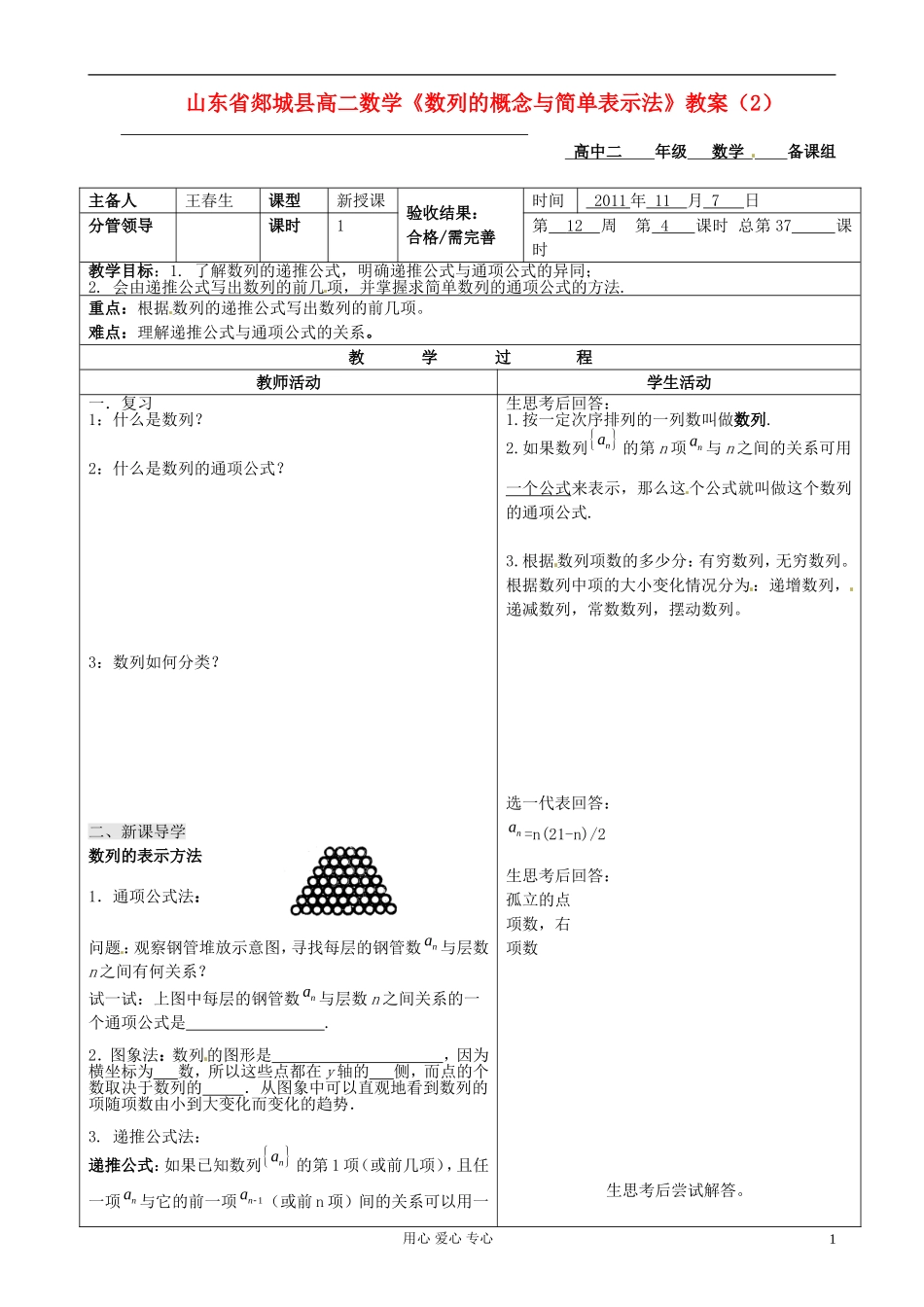
山东省郯城县高二数学《数列的概念与简单表示法》教案(2) 高中二 年级 数学 备课组主备人王春生课型新授课验收结果:合格/需完善时间 2011 年 11 月 7 日分管领导课时1第 12 周 第 4 课时 总第 37 课时 教学目标:1. 了解数列的递推公式,明确递推公式与通项公式的异同;2. 会由递推公式写出数列的前几项,并掌握求简单数列的通项公式的方法. 重点:根据数列的递推公式写出数列的前几项。难点:理解递推公式与通项公式的关系。教 学 过 程教师活动学生活动一.复习1:什么是数列?2:什么是数列的通项公式?3:数列如何分类?二、新课导学数列的表示方法1.通项公式法:问题:观察钢管堆放示意图,寻找每层的钢管数na 与层数n 之间有何关系?试一试:上图中每层的钢管数na 与层数 n 之间关系的一个通项公式是 . 2.图象法:数列的图形是 ,因为横坐标为 数,所以这些点都在 y 轴的 侧,而点的个数取决于数列的 .从图象中可以直观地看到数列的项随项数由小到大变化而变化的趋势.3. 递推公式法:递推公式:如果已知数列 na的第 1 项(或前几项),且任一项na 与它的前一项1na (或前 n 项)间的关系可以用一生思考后回答:1.按一定次序排列的一列数叫做数列.2.如果数列 na的第 n 项na 与 n 之间的关系可用一个公式来表示,那么这 个公式就叫做这个数列的通项公式.3.根据数列项数的多少分:有穷数列,无穷数列。根据数列中项的大小变化情况分为:递增数列,递减数列,常数数列,摆动数列。选一代表回答:na =n(21-n)/2生思考后回答:孤立的点项数,右项数生思考后尝试解答。用心 爱心 专心1个公式来表示,那么这个公式就叫做这个数列的递推公式. 试试:上图中相邻两层的钢管数na 与1na 之间关系的一个递推公式是 . 4. 列表法:试试:上图中每层的钢管数na 与层数 n 之间关系的用列表法如何表示?所有数列都能有四种表示方法吗?例 1 设数列 na满足11111(1).nnaana 写出这个数列的前五项. 变式:已知12a ,12nnaa ,写出前 5 项,并猜想通项公式na . 例 2 已知 数列 na满足10a ,12nnaan , 那么2007a( ).A. 2003×2004 B. 2004×2005 C. 2007×2006 D. 22004练 1. 已 知 数 列 na满 足11a ,223a , 且111120nnnnnnaaa aaa(2n ...