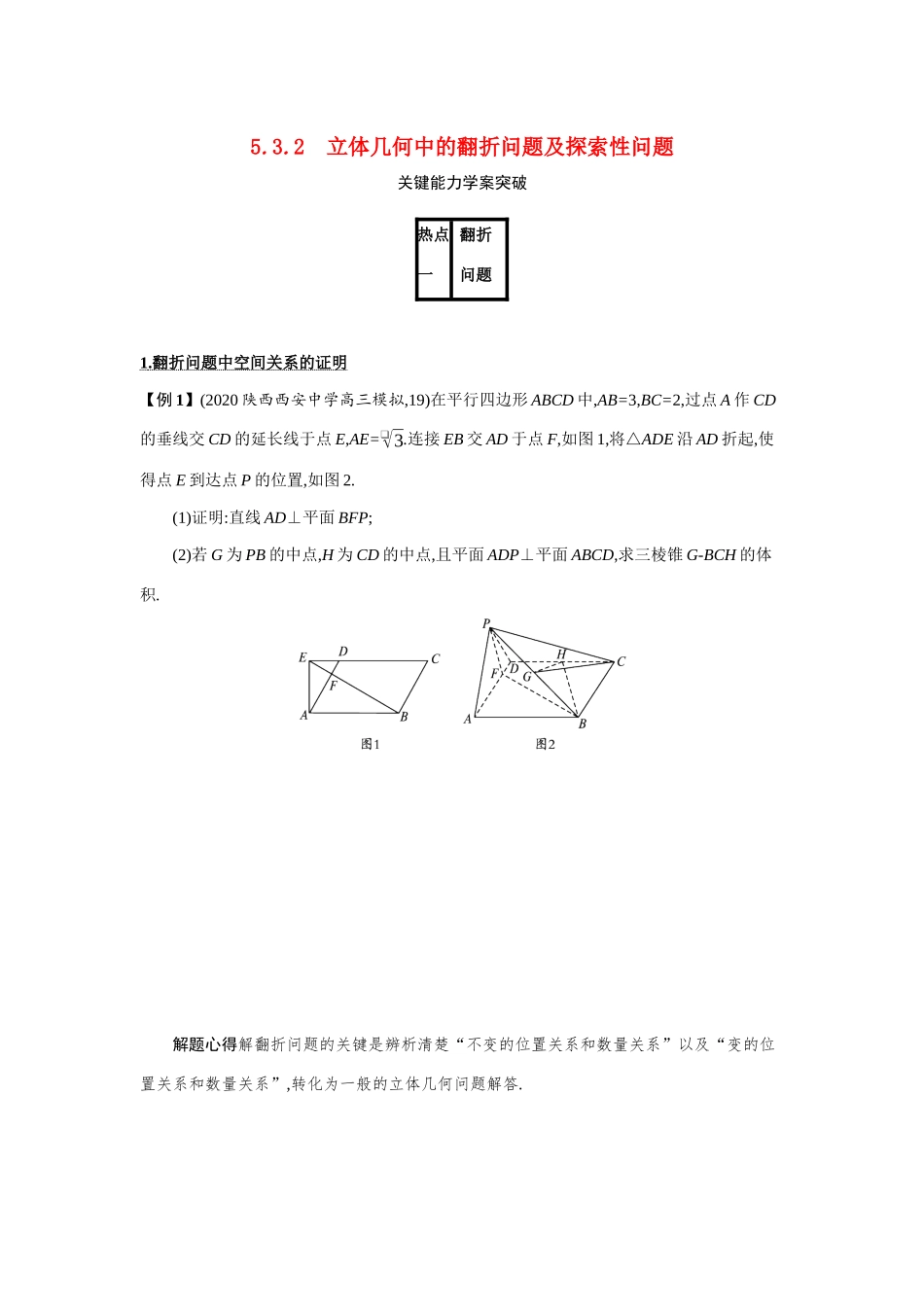
5.3.2 立体几何中的翻折问题及探索性问题关键能力学案突破热点一翻折问题1 . 翻折问题中空间关系的证明 【例 1】(2020 陕西西安中学高三模拟,19)在平行四边形 ABCD 中,AB=3,BC=2,过点 A 作 CD的垂线交 CD 的延长线于点 E,AE=❑√3.连接 EB 交 AD 于点 F,如图 1,将△ADE 沿 AD 折起,使得点 E 到达点 P 的位置,如图 2.(1)证明:直线 AD⊥平面 BFP;(2)若 G 为 PB 的中点,H 为 CD 的中点,且平面 ADP⊥平面 ABCD,求三棱锥 G-BCH 的体积.解题心得解翻折问题的关键是辨析清楚“不变的位置关系和数量关系”以及“变的位置关系和数量关系”,转化为一般的立体几何问题解答.【对点训练 1】(2020 湖南怀化三模,18)图 1 是直角梯形ABCD,AB∥DC,∠D=90°,AB=2,DC=3,AD=❑√3,点 E 在 DC 上,CE=2ED,以 BE 为折痕将△BCE折起,使点 C 到达点 C1的位置,且 AC1=❑√6,如图 2.(1)证明:平面 BC1E⊥平面 ABED;(2)求点 B 到平面 AC1D 的距离.2 . 求翻折问题中的空间角 【例 2】(2020 北京顺义二模,17)如图 1 所示,四边形 ABCD 是边长为❑√2的正方形,沿 BD 将点C 翻折到点 C1位置(如图 2 所示),使得二面角 A-BD-C1成直二面角.E,F 分别为 BC1,AC1的中点.(1)求证:BD⊥AC1;(2)求平面 DEF 与平面 ABD 所成的二面角的余弦值.解题心得平面图形翻折后成为空间图形,翻折后还在同一个平面上的线线关系不发生变化,不在同一个平面上的可能发生变化.解决这类问题就是要根据这些变与不变,去研究翻折以后的空间图形中的线面关系和各类几何量的度量值.【对点训练 2】(2020 山东济宁三模,18)如图 1,四边形 ABCD 为矩形,BC=2AB,E 为 AD 的中点,将△ABE,△DCE 分别沿 BE,CE 折起得图 2,使得平面 ABE⊥平面 BCE,平面 DCE⊥平面BCE.(1)求证:平面 ABE⊥平面 DCE;(2)若 F 为线段 BC 的中点,求直线 FA 与平面 ADE 所成角的正弦值.热点二探索性问题1 . 与空间位置关系有关的探索性问题 【例 3】(2020 天津河西一模,17)在如图所示的几何体 P-ABCDE 中,△ABP 和△AEP 均为以 A为直角顶点的等腰直角三角形,AB⊥AE,AB∥CE,AE∥CD,CD=CE=2AB=4,M 为 PD 的中点.(1)求证:CE⊥PE;(2)求二面角 M-CE-D 的大小;(3)在线段 PE 上是否存在点 N,使得平面 ABN∥平面 MCE,若存在,求出线段 AN 的长;若不存在,请说明理由.解题心得 1.对于空间位置关系中的存在性问题,解题思路是...