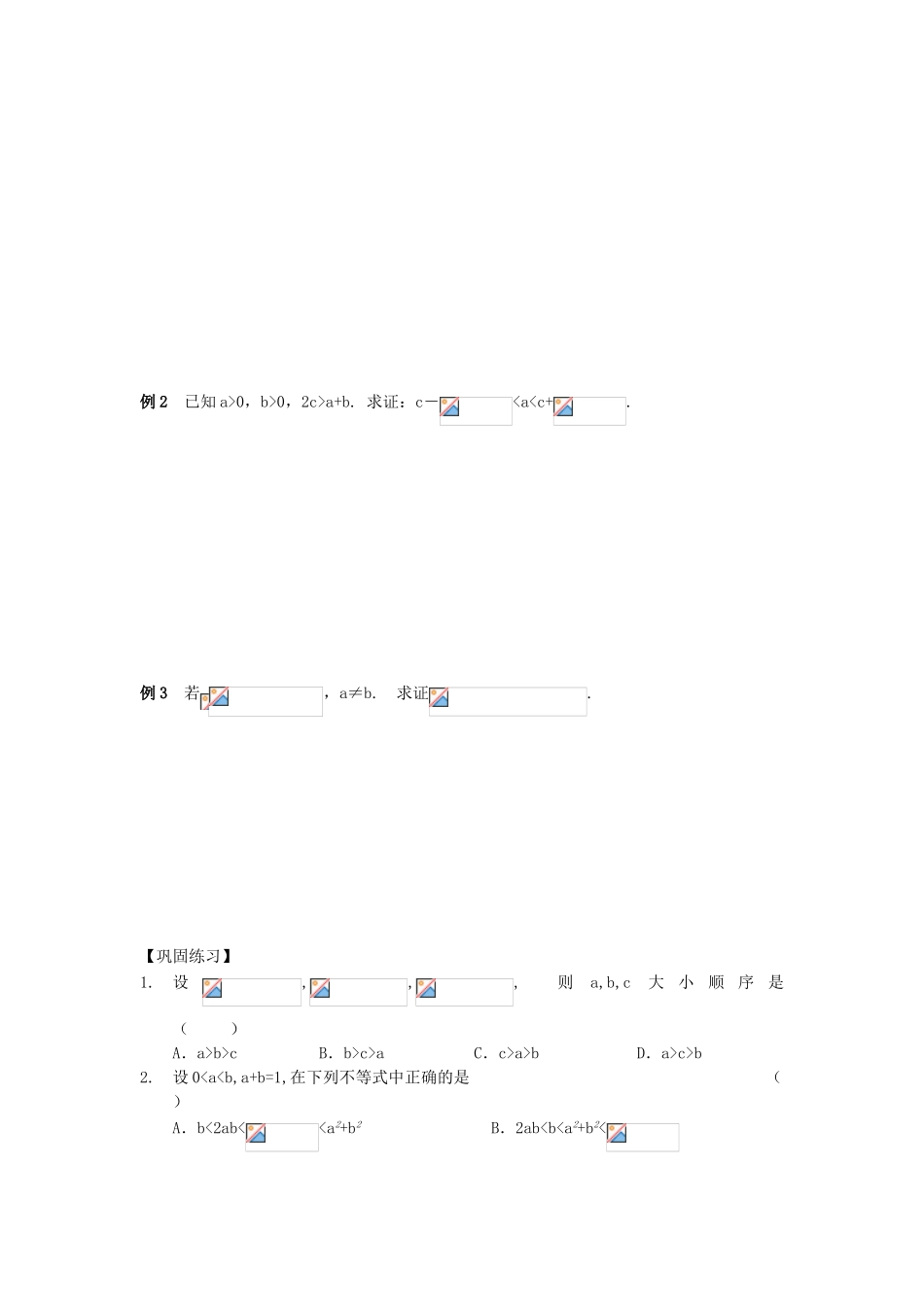
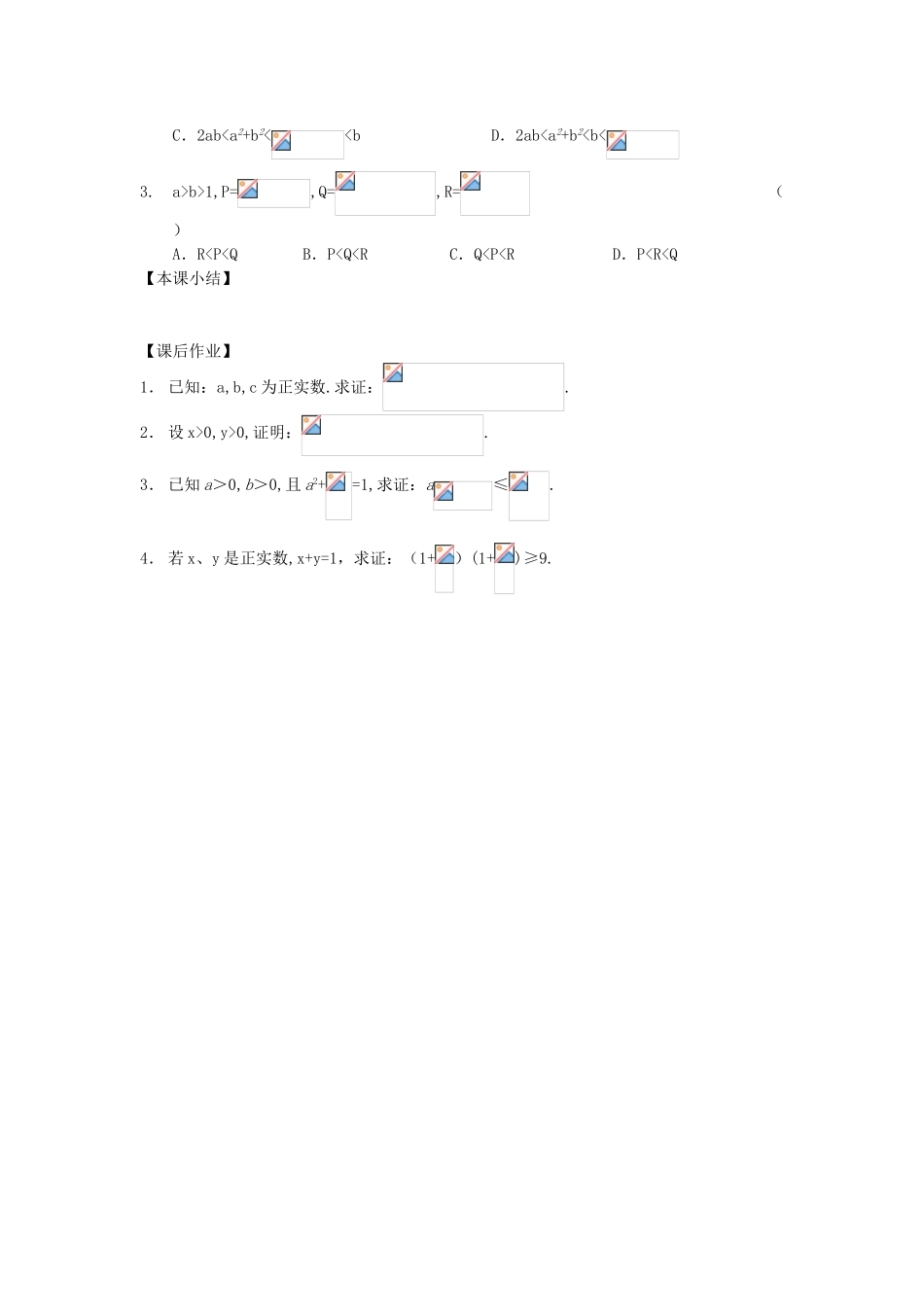
§6.2 综合法和分析法证明不等式【复习目标】1. 熟悉证明不等式的综合法、分析法,并能应用其证明不等式;2. 理解分析法的实质是“执果索因”;注意用分析法证明不等式的表述格式;3. 对于较复杂的不等式,能综合使用各种方法给予证明。【重点难点】 综合法的难点在于从何处出发进行论证并不明确,因此我们经常用分析法寻找解题的思路,再用综合法表述。分析法是“执果索因”,综合法是“由因导果”。要注意分析法的表述格式。【课前预习】1. “a>1”是“”的 ( )A. 充分但不必要条件 B. 必要但不充分条件 C. 充要条件 D. 既不充分也不必要条2.证明3.证明 a2+b2+c2≥ab+bc+ac.4.设 a,b,c∈R+,则三个数,,的值,则 ( )A. 都大于 2 B. 至少有一个不大于 2 C. 都小于 2 D. 至少有一个不小于2【典型例题】例 1 (1)已知,且,求证:; (2)设 a,b,c 都是正数,求证:.例 2 已知 a>0,b>0,2c>a+b. 求证:c-
b>c B.b>c>a C.c>a>b D.a>c>b2.设 0b>1,P=,Q=,R= ( )A.R0,y>0,证明:.3. 已知 a>0,b>0,且 a2+=1,求证:a≤.4. 若 x、y 是正实数,x+y=1,求证:(1+)(1+)≥9.