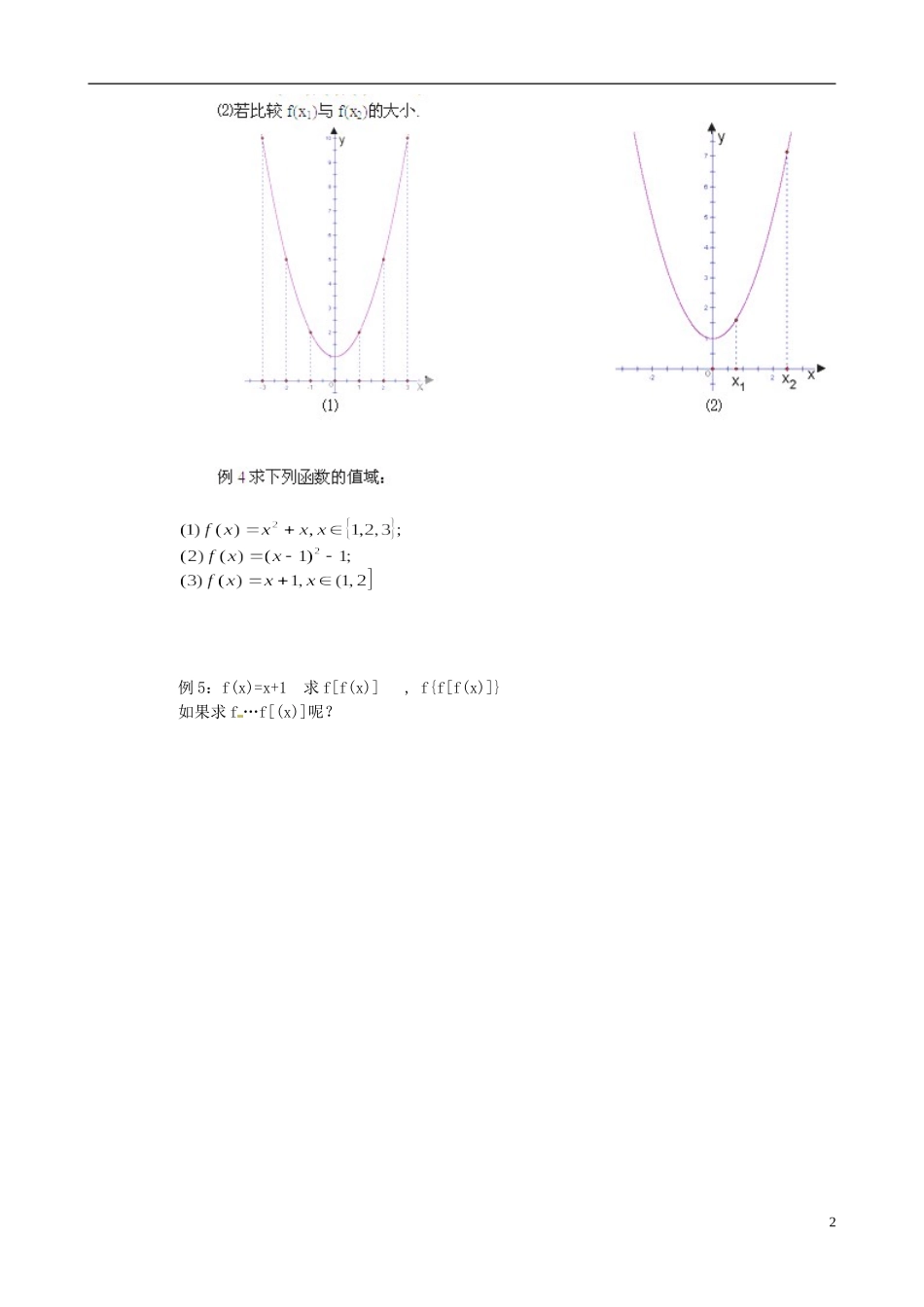
江苏省南京市第三中学高中数学 §2.1.1 函数的概念和图象⑵教案 苏教版必修 1课 题:§2.1.1 函数的概念和图象⑵教学目标:1.在实际情境中,了解图象法是描述两个变量之间函数关系的一种重要方法;2.从集合的角度了解函数图象的概念,从形的角度进一步加深对函数概念的理解;3.了解函数的图象不仅可以是连续的曲线,也可以是一些孤立的点或其它形式.重点难点:重点——函数图象的概念;难点——理解函数图象可能是一些孤立的点.教学教程:一、问题情境问题 1:在我们的日常生活、学科教学中,哪些地方用到了函数的图象?二、学生活动可以在课前布置学生通过报纸、杂志、网络及在其它学科的课本中,寻找一些函数图象的实例,并在课堂上展示.其 实 在 初 中 我 们 已 经 研 究 过 函 数 的 图 象 , 了 解 了 一 次 函 数 y=kx+b 、 二 次 函 数y=ax2+bx+c(a≠0)、反比例函数 y=(k≠0)的图象.问题 2:前面我们已经用集合的观点重新定义了函数的概念,那么大家能用集合的观点来定义函数图象的概念吗?学生如果课前预习了,可能说出函数图象的定义,但不完整,可以让其他学生进行补充,只有学生都不能完整说出函数图象的概念时,才适当点拨,最后由师生共同得到函数图象的定义.三、建构数学函数图象的定义:将自变量的一个值 x0作为横坐标,相应的函数值 f(x0)作为纵坐标,就得到坐标平面上的一个点(x0,f(x0)).当自变量取遍函数定义域 A 中的每一个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,f(x))|x∈A},即 {(x,y)|y=f(x),x∈A},所有这些点组成的图形就是函数 y=f(x)的图象.在初中我们已经画过一次函数 y=kx+b、二次函数 y=ax2+bx+c(a≠0)、反比例函数y=(k≠0)的图象,知道它们的图象分别是直线、抛物线、双曲线.例 1 画出下列函数的图象,并由图象求出函数的值域.⑴f(x)= x-1⑵f(x)= (x-1)2+1,x∈[-1,2)解:描点作出图象,分别如下图所示.⑴⑵问题 3:所有函数的图象一定是连续的直线或者曲线吗?例 2 在 P21 的第一个实例中,如果把人口数(百万人)看作是年份的函数,请根据此实例中的表画出这个函数的图象.此函数图象是一群孤立的点.四、数学运用1.例题例 3 画出函数 f(x)=x2+1 的图象,并根据图象回答下列问题:1较 f(-2),f(1),f(3)的大小;1例 5:f(x)=x+1 求 f[f(x)] , f{f[f(x)]}如果求 f …f[(x)]呢?2例 6:(1)已知 f(x)=x+1 求 f(x+1) , f(x-1)(2)已知 f(x+1)=x+2 求 f(x...