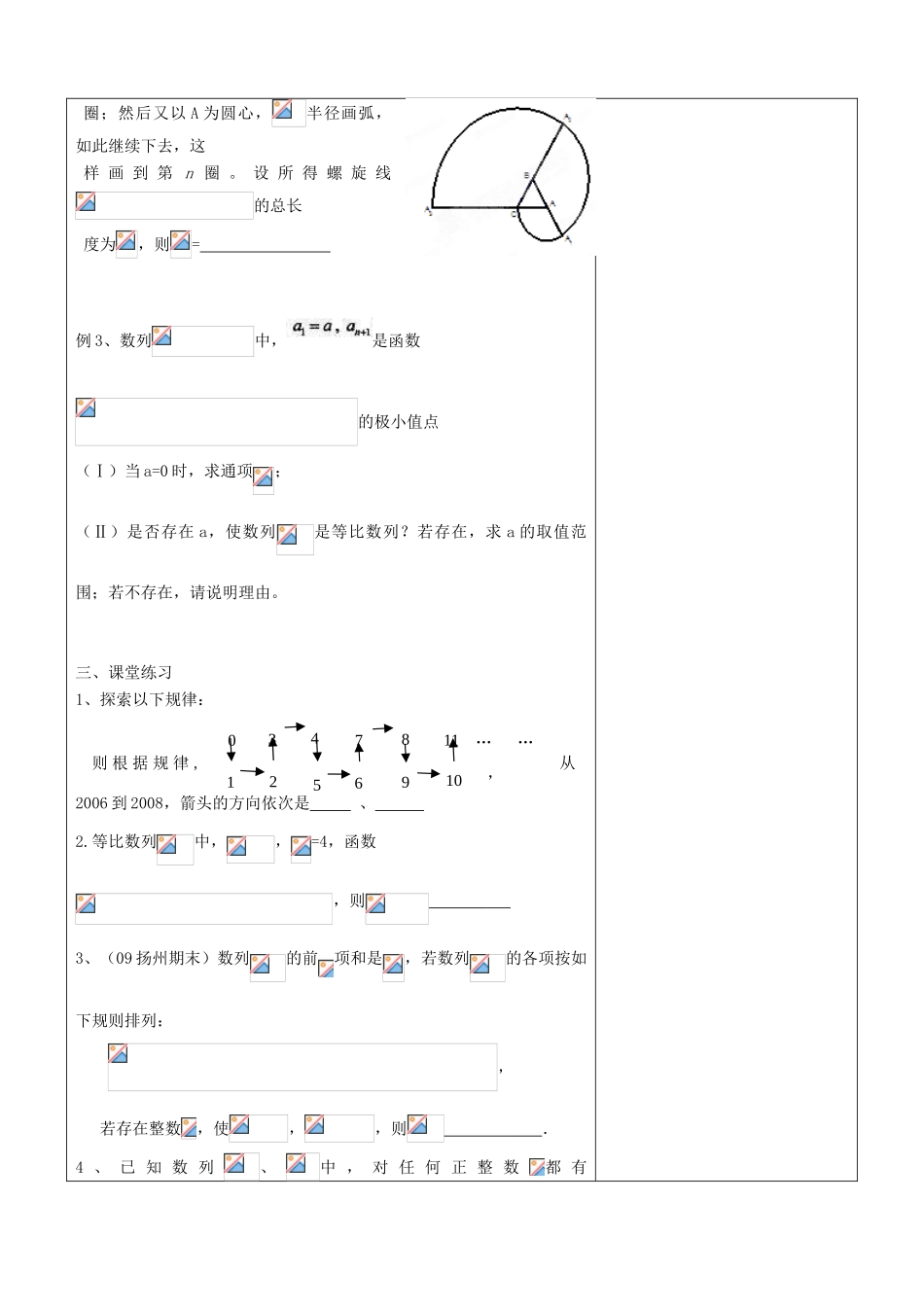
( 第3题 )课题 §23 等差、等比的运用(2)课型复习课上课时间20 年 月 日教学目标1、能熟练、灵活运用等差数列、等比数列的通项公式和前项和公式解决有关问题;2、能在具体的问题情境中识别等差、等比数列关系,并能用有关知识解决相应的问题。重点难点重点:运用等差数列、等比数列的通项公式和前项和公式难点:在具体的问题情境中识别等差、等比关系,并能解决相应的问题教学过程记录一、基础训练1、(08 江苏)如图,将全体正整数排成三角形数阵:则根据以上的排列规律,第(3)行从左向右第 3 个数是 2、下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第 n 个图案中需用黑色瓷砖________块.(用含 n 的代数式表示)3、某人今年年初向银行申请个人住房公积金贷款 20 万元购买住房,月利率为,按复利计算,每月等额还贷一次,并从贷款后的次月初开始还贷。如果 10 年还清,那么每月应还贷 元(用表示)二、典型例题例 1、如图所示的三角形数阵中,满足:(1)第 1 行的数为 1;(2)第 n(n≥2)行首尾两数均为 n,其余的数都等于它肩上的两个数相加,则第行中第 2 个数是 (用 n 表示).例 2、如图所示的螺旋线是用以下方法画成的,是边长为 a 的 正 三 角 形 , 曲 线分 别 是为 圆 心 ,为半径画的弧,曲线称为螺旋线的第一 12 34 5 67 8 9 1011 12 13 14 15圈;然后又以 A 为圆心,半径画弧,如此继续下去,这样 画 到 第 n 圈 。 设 所 得 螺 旋 线的总长 度为,则= 例 3、数列中,是函数的极小值点(Ⅰ)当 a=0 时,求通项; (Ⅱ)是否存在 a,使数列是等比数列?若存在,求 a 的取值范围;若不存在,请说明理由。三、课堂练习1、探索以下规律:则 根 据 规 律 , 从2006 到 2008,箭头的方向依次是 、 2.等比数列中,,=4,函数,则 3、(09 扬州期末)数列的前项和是,若数列的各项按如下规则排列:,若存在整数,使,,则 .4 、 已 知 数 列、中 , 对 任 何 正 整 数都 有1256791011…… ,0348. 1)若数列是首项和公差都是 1 的等差数列,求证:数列是等比数列; 2)若数列是等比数列,数列是否是等差数列,若是请求出通项公式,若不是请说明理由;学后反思(通过这节课的学习活动你有哪些收获?还有什么困惑?)