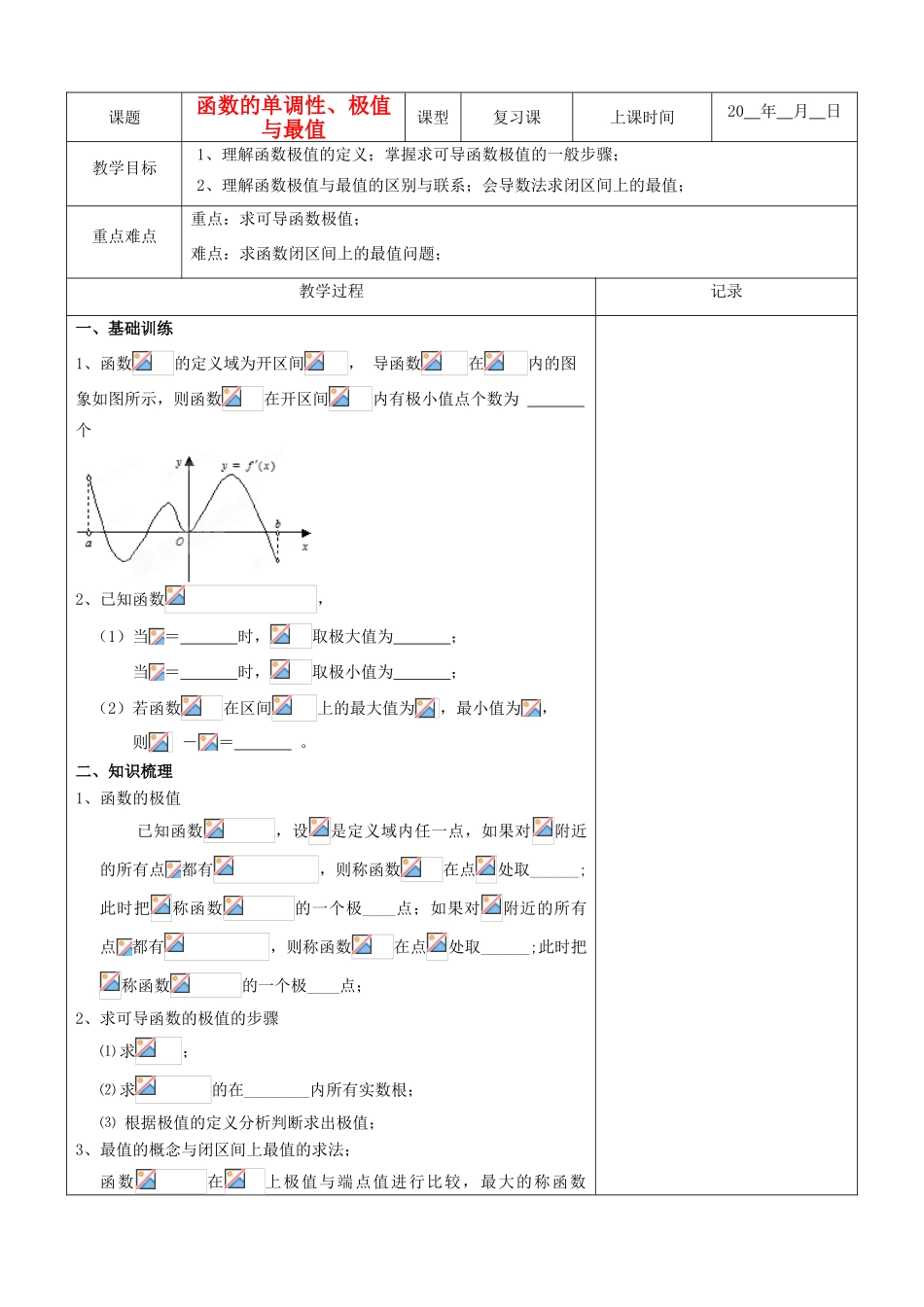
课题函数的单调性、极值与最值课型复习课上课时间20 年 月 日教学目标1、理解函数极值的定义;掌握求可导函数极值的一般步骤;2、理解函数极值与最值的区别与联系;会导数法求闭区间上的最值;重点难点重点:求可导函数极值;难点:求函数闭区间上的最值问题;教学过程记录一、基础训练1、函数的定义域为开区间, 导函数在内的图象如图所示,则函数在开区间内有极小值点个数为 个2、已知函数,(1)当= 时,取极大值为 ;当= 时,取极小值为 ;(2)若函数在区间上的最大值为,最小值为,则 -= 。二、知识梳理1、函数的极值 已知函数,设是定义域内任一点,如果对附近的所有点都有,则称函数在点处取______;此时把称函数的一个极____点;如果对附近的所有点都有,则称函数在点处取______;此时把称函数的一个极____点;2、求可导函数的极值的步骤 ⑴ 求;⑵ 求的在________内所有实数根;⑶ 根据极值的定义分析判断求出极值;3、最值的概念与闭区间上最值的求法;函数在上极值与端点值进行比较,最大的称函数在的最大值,最小的称函数在的最小值;三、例题讲解例 1、⑴求函数的极值;⑵ 已知函数;试求的极大值,极小值点;例 2、求函数在区间上的最大值。例 3、设,函数;当时,求函数的最小值;四、课堂练习1、奇函数在处有极值,则 3的值为_____2、《数学之友》P191 课前预习的第 3、7、8;3、已知函数在处取得极大值,在 处取得极小值,且.(1)证明: ; (2)求 z = a+2 b 的取值范围。五、小结与作业1、《数学之友》白皮书 P145 基础训练的 3、4、6、8、9;2、《数学之友》白皮书 P145-P146 能力强化的 3、4、5、6、8;3、《数学之友》白皮书 P145-P146 感受高考的 1、2、4、7;学后反思(通过这节课的学习活动你有哪些收获?还有什么困惑?)