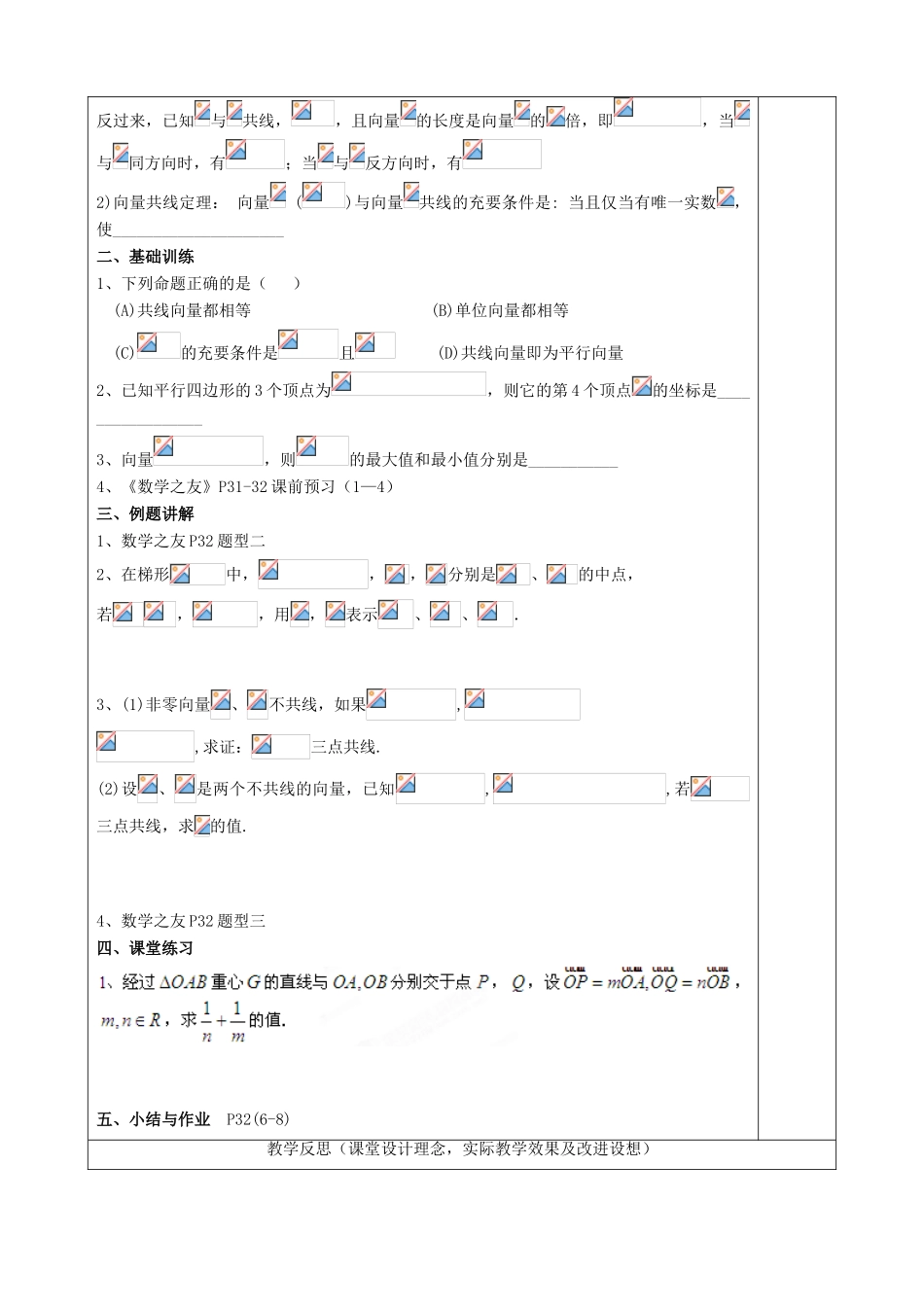
课题平面向量的概念及线性运算总备课第 28 课时教学目标1、理解向量的有关概念.2、掌握向量的加法、减法、数乘及其运算法则.3、理解向量共线的充要条件.4、会用向量的代数运算法则、三角形法则、平行四边形法则解决有关问题.重点难点教学过程记 录一、知识梳理1. 向量的概念:① 数学中我们把既有_____又有______的量叫向量(比物理里的矢量更直接)② 长度为 0 的向量叫____向量; 长度为 1 个单位长度的向量,叫____向量③ 方向相同或相反的非零向量叫_____向量;也叫_______向量(因为平行向量都可移到同一直线上)④ 长度相等且方向相同的向量叫____________ 思辩 1)平行向量是否一定方向相同?( )2)不相等的向量是否一定不平行? ( )3)与零向量相等的向量必定是_____向量4)与任意向量都平行的向量是______向量2.向量的线性运算① 加法:(作图)1)三角形法则 2)平行四边形法则向量加法的满足交换律:____________ 结合律:_______________② 减法: 与 、 向量,叫做的相反向量,记作零向量的相反向量是 , ______ 若与互为相反向量,则,③ 数乘:实数与向量的积是一个_____,记作_______,它的模与方向规定如下:1)_______________④>0时,的方向与___的方向相同;当<0时, 的方向与______的方向相反; 运算律:______;=_________; =________3.向量共线的充要条件1)向量 ()、,如果有一个实数,使,则与_______反过来,已知与共线,,且向量的长度是向量的倍,即,当与同方向时,有;当与反方向时,有2)向量共线定理: 向量 ()与向量共线的充要条件是: 当且仅当有唯一实数,使_____________________二、基础训练1、下列命题正确的是( )(A)共线向量都相等 (B)单位向量都相等 (C)的充要条件是且 (D)共线向量即为平行向量2、已知平行四边形的 3 个顶点为,则它的第 4 个顶点的坐标是_________________3、向量,则的最大值和最小值分别是___________4、《数学之友》P31-32 课前预习(1—4)三、例题讲解1、数学之友 P32 题型二2、在梯形中,,,分别是、的中点,若,,用,表示、、.3、(1)非零向量、不共线,如果,,求证:三点共线.(2)设、是两个不共线的向量,已知,,若三点共线,求的值. 4、数学之友 P32 题型三四、课堂练习五、小结与作业 P32(6-8)教学反思(课堂设计理念,实际教学效果及改进设想)