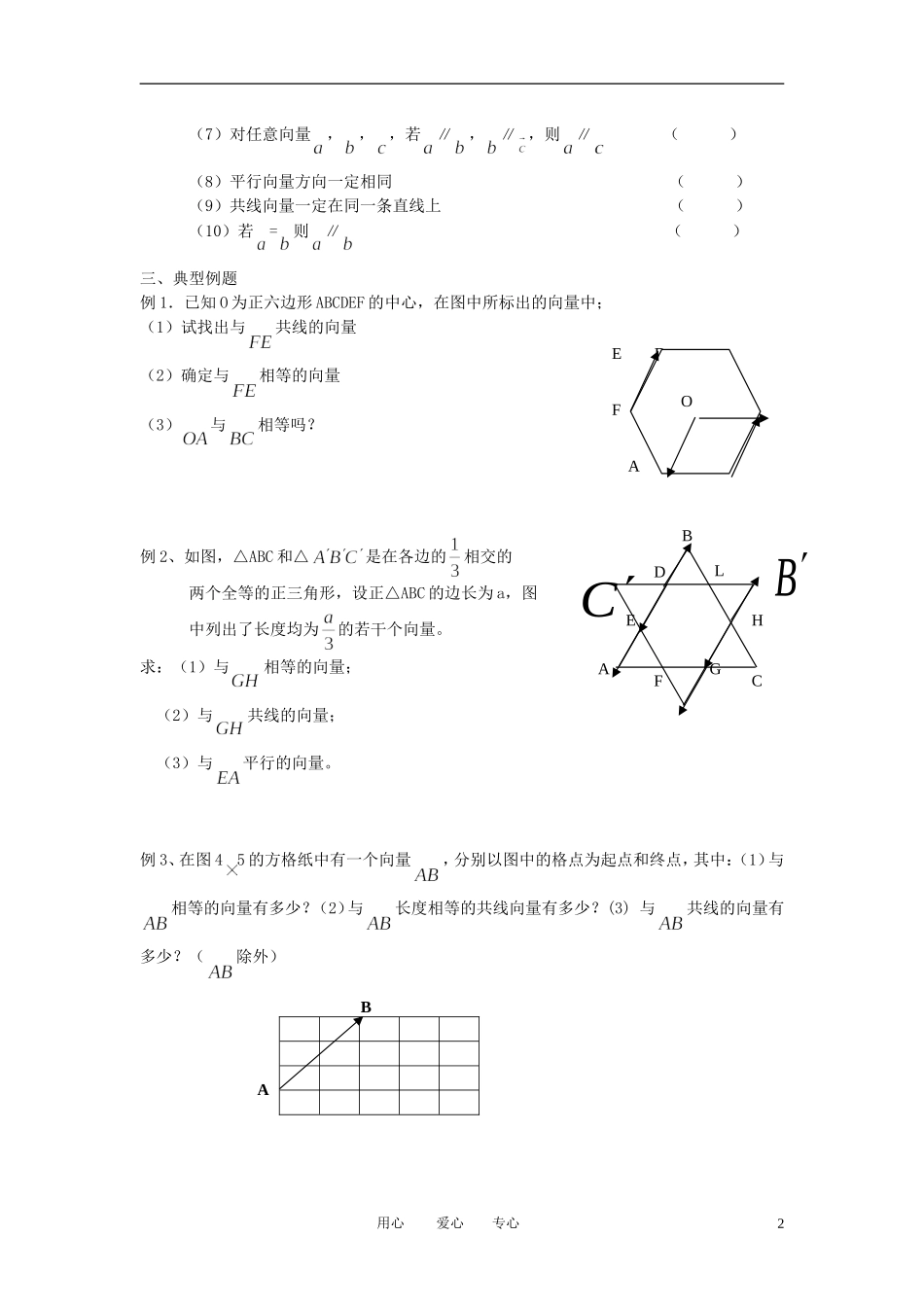
课时 1 向量的概念及表示【学习目标】要求学生掌握向量的意义、表示方法以及有关概念,并能作一个向量与已知向量相等,根据图形判定向量是否平行、共线、相等。一、知识梳理1.数量:仅用一个实数就可以表示的量叫数量。如距离、时间、面积等。2. 向量: 叫向量。如物理中的位移、速度、力等。3.向量的表示:常用一条有向线段来表示,有向线段的长度表示向量的大小,箭头表示所指的方向。以 A 为起点。以 B 为终点的向量记为,也可以用来表示。如注:两个向量的模可以比较大小,但向量不能比较大小。4.向量的 叫向量的模。记为5.特殊向量:零向量: 单位向量: 6、平行向量: 规定:零向量与任一向量平行7、相等向量: 8、共线向量:任意一组平行向量都可以平移到同一条直线上。 故平移向量又称共线向量9、相反向量:我们把与 的向量叫做的相反向量- 规定:零向量的相反向量仍是零向量二、基础训练1.下列各题中,哪些是数量,哪些是向量?质量,密度,角,位移,距离,浮力,速度,功,加速度,温度,电流强度,浓度,向心力2.判断下列说法是否正确,并说明理由。(1)温度有零上和零下之分。所以温度是向量 ( )(2) =0 ( )(3)共线向量就是平行向量 ( )(4)若,为非零向量,且=,则= ( )(5)若=-则∥ ( )(6)对任意向量,,,若=,=,则= ( )用心 爱心 专心1ABac(7)对任意向量,,,若∥,∥ ,则∥ ( )(8)平行向量方向一定相同 ( )(9)共线向量一定在同一条直线上 ( )(10)若=则∥ ( )三、典型例题例 1.已知 O 为正六边形 ABCDEF 的中心,在图中所标出的向量中;(1)试找出与共线的向量(2)确定与相等的向量(3)与相等吗?例 2、如图,△ABC 和△是在各边的相交的两个全等的正三角形,设正△ABC 的边长为 a,图中列出了长度均为的若干个向量。求:(1)与相等的向量;(2)与共线的向量; (3)与平行的向量。例 3、在图 45 的方格纸中有一个向量,分别以图中的格点为起点和终点,其中:(1)与相等的向量有多少?(2)与长度相等的共线向量有多少?(3) 与共线的向量有多少?(除外) 用心 爱心 专心2E DF o C A BOHGFEDCABLBCAB三.课后作业:1、下列命题中,正确的是 A B C D 2、下列命题中真命题为 ① 向量的长度与向量的长度相等;②,则的方向相同或相反;③ 两个有共起点且相等的向量,其终点必相同;④两个有共...