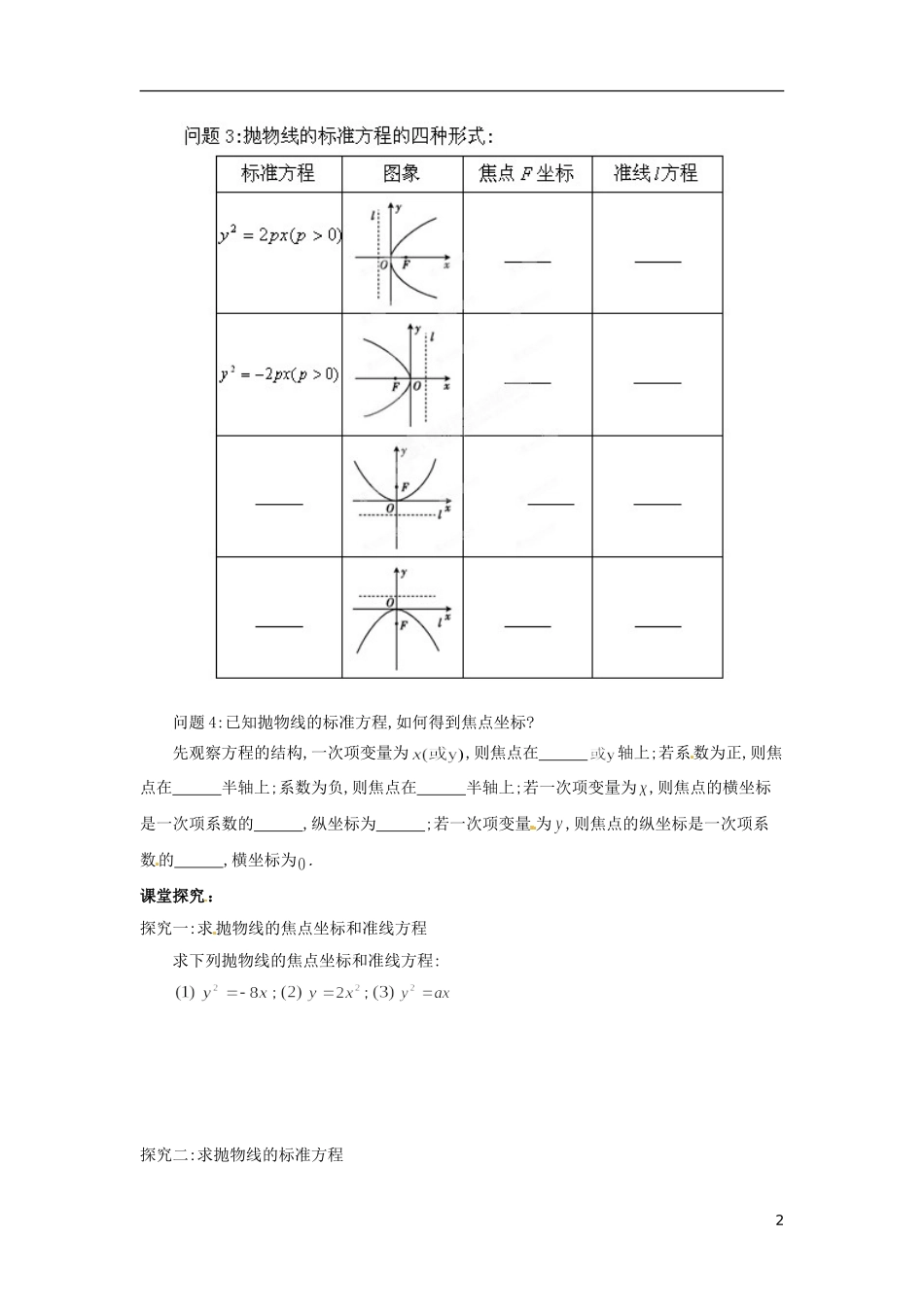
江苏省响水中学高中数学 第 2 章《圆锥曲线与方程》抛物线标准方程1 导学案 苏教版选修 1-1学习目标:1.掌握抛物线定义、标准方程及其几何图形.能用待定系数法求抛物线的 标准方程.2.理解标准方程中 与抛物线的开口方向、焦点位置的关系.3.亲自体验由具体的演示实验探寻出一般数学结论的过程,体会探究的乐趣, 激发学生的学习热情.学习运用类比的思想探寻另三种标准方程.重点:抛物线的定义和标准方程难点:抛物线标准方程推导过程的组织和引导,以及如何类比发现另三种形式 的标准方程课前预习:如图,把一根直尺固定在画图板内直尺 的位置上,截取一根绳子的长度等于的长度,现将绳子的一端固定在三角板的顶点处,另一端用图钉固定在处;用一支粉笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺上下滑动,这样粉笔就描出一条曲线.问题 1:在上述情境中,点到点与点到直线 的距离 .(填相等或不相等),理由是 . 问题 2:平面内与一个定点和一条定直线 ( 不经过)的距离 的点的轨迹叫作抛物线.点叫作抛物线的 ,定直线 叫作抛物线的准线.如果定义中不加上条件“ 不经过”,即若点在直线 上,满足条件的动点的轨迹是 ,而不是抛物线. 1 问题 4:已知抛物线的标准方程,如何得到焦点坐标?先观察方程的结构,一次项变量为,则焦点在 轴上;若系数为正,则焦点在 半轴上;系数为负,则焦点在 半轴上;若一次项变量为 ,则焦点的横坐标是一次项系数的 ,纵坐标为 ;若一次项变量 为,则焦点的纵坐标是一次项系数的 ,横坐标为 . 课堂探究:探究一:求抛物线的焦点坐标和准线方程求下列抛物线的焦点坐标和准线方程:;;探究二:求抛物线的标准方程2(1)已知抛物线的焦点在 y 轴上,并且经过点,求抛物线的标准方程;(2)已知抛物线的焦点在坐标轴上,且抛物线过点,求它的标准方程.探究三:求动点的轨迹方程若动点到点 F的距离比它到直线的距离小,求动点的轨迹方程.课堂检测:34