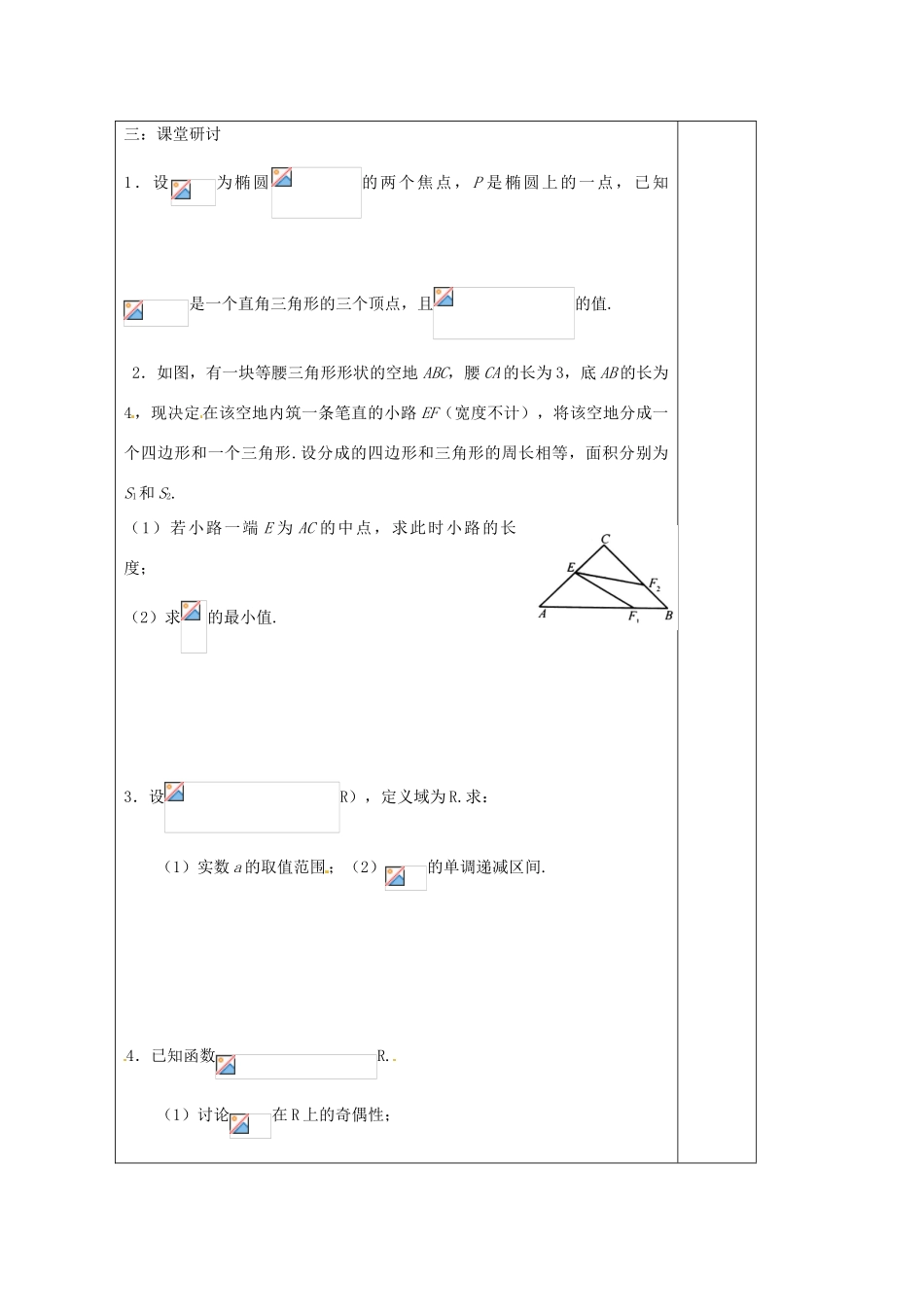
江苏省建陵高级中学 2014 届高考数学二轮复习 专题 11 分类讨论思想导学导学案一:高考趋势分类讨论思想就是根据所研究对象的性质差异,区分不同的情况予以分析解决.需分类讨论的试题覆盖较多的知识点,有利于考查学生知识理解的深度和能力的水平.纵观近几年高考试卷,均涉及分类讨 论思想方法的考查.试题中既有灵活多变的客观性试题 ,又有能力要求很高的主观性试题.常见的分类情形有:按数的特性分类,按字母的取值范围分类,按事件的可能情况分类,按图形的位置特征分类等.分类讨论思想 方法仍将是高考重点考查的内容之一.二:课前预习1.已知集合,则 a 的值为 .2 . 双 曲 线 的 渐 近 线 方 程 为, 则 该 双 曲 线 的 离 心 率 等 于 .3.已知直线 l 过点 P(-2,1),点 A(-1,-2)到直线 l 的距离等于 1,则直线 l 的方程为 .4.正三棱柱的侧面展开图是边长分别为 2 和 4 的矩形,则它的体积为 .5.设函数对任意的恒成立,则实数 m 的取值范围是 .6 . 已 知 函 数上 是 单 调 函 数 , 且,则 备 注三:课堂研讨1.设为椭圆的两个焦点, P 是椭圆上的一点,已知是一个直角三角形的三个顶点,且的值.2.如图,有一块等腰三角形形状的空地 ABC,腰 CA 的长为 3,底 AB 的长为4,现决定在该空地内筑一条笔直的小路 EF(宽度不计),将该空地分成一个四边形和一个三角形.设分成的四边形和三角形的周长相等,面积分别为S1和 S2.(1)若小路一端 E 为 AC 的中点,求此时小路的长度;(2)求的最小值.3.设R),定义域为 R.求:(1)实数 a 的取值范围;(2)的单调递减区间.4.已知函数R.(1)讨论在 R 上的奇偶性;(2)当时,求函数在闭区间上的最大值.四:课后反思课堂检测——分类讨论思想方法 姓名: 1.设=B,则实数 a= ..2.设函数= .3.已知椭圆 .4.行列式的所有可能的值中,最大的是 .5.已知函数的定义域为Z),值域为[0,1],则满足条件的整数对共有 对.6.将两颗骰子先后各抛一次,表示抛甲、乙两颗骰子所得的点数.(1)若点落在不等式组表示的平面区域内的 事件为 A,求P(A);(2)若点落在直线上,且使此事件的概率最大,求 m 的值.课外作业——分类讨论思想方法 姓名: 1 . 已 知 函 数的 切 线 过 点 ( 1 , 2 ) , 则 此 切 线 的 方 程 .2.已知 t 为常数,函数在区间[0,3]上的最大...