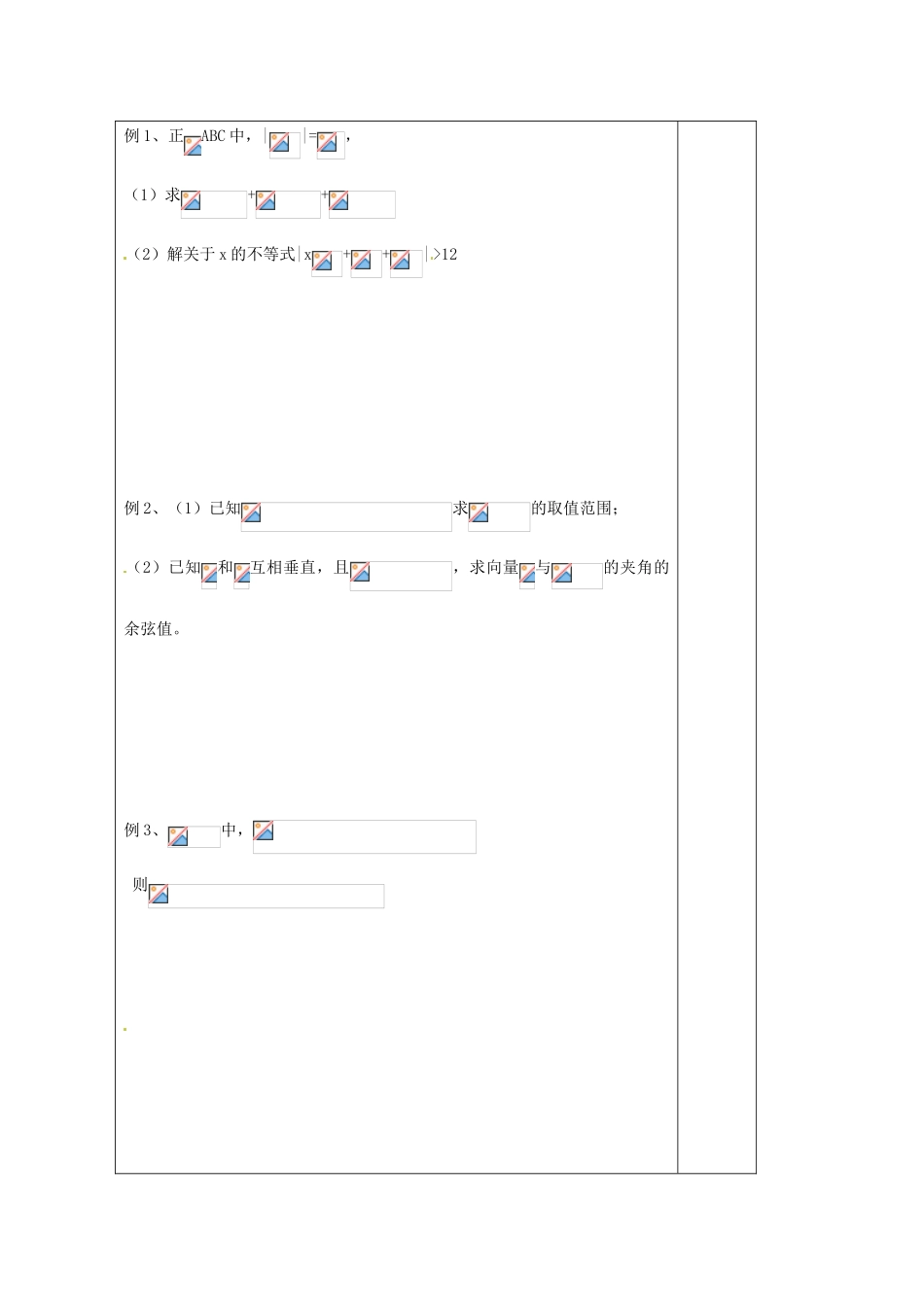
江苏省建陵高级中学 2014 届高考数学一轮复习 向量的数量积导学案(1)一:学习目标理解:向量的数量积的几何表示与坐标表示及数量积的运算律;掌握:向量数量积的重要性质,会利用数量积求向量的夹角与模。二:课前预习1、已知的夹角为,2、已知,则3、设是非零向量,且相互不共线,给出下列命题:①; ②;③; ④若,则;⑤,其中正确命题的序号为__________________.4、已知(-)(2+)=-4,||=2,||=4,则与的夹角为 .5、已知=(4,-3),||=1,=5,则= .6、在ABC 中,①若>0,则ABC 的形状是 . ② 若,则ABC 的形状是 ③ 若,则.三:课堂研讨备 注例 1、正ABC 中,||=,(1)求++(2)解关于 x 的不等式|x++|>12例 2、(1)已知求的取值范围;(2)已知和互相垂直,且,求向量与的夹角的余弦值。例 3、中,则课堂检测——向量的数量积(1) 姓名: 1.已知 a=(2,3),b=(-4,7),则 a 在 b 方向上的投影为 .2.在边长为 1 的正三角形 ABC 中,设=a,=c,=b,则 a·b+b·c+c·a= .3.向量 a=(cos15°,sin15°),b=(-sin15°,-cos15°),则|a-b|的值是 .4.已知向量 a=b=且 x∈.(1)求 a·b 及|a+b|;(2)若 f(x)=a·b-|a+b|,求 f(x)的最大值和最小值.课外作业——向量的数量积(1) 姓名: 1.已知向量 a=(2,1),b=(3,) (>0),若(2a-b)⊥b,则= .2.已知 a、b 是平面内两个互相垂直的单位向量,若向量 c 满足(a-c)·(b-c)=0,则|c|的最大值是 .3.已知 a=(cos,sin),b=(cos,sin)(0<<<).(1)求证:a+b 与 a-b 互相垂直;(2)若 ka+b 与 a-kb 的模相等,求-.(其中 k 为非零实数)