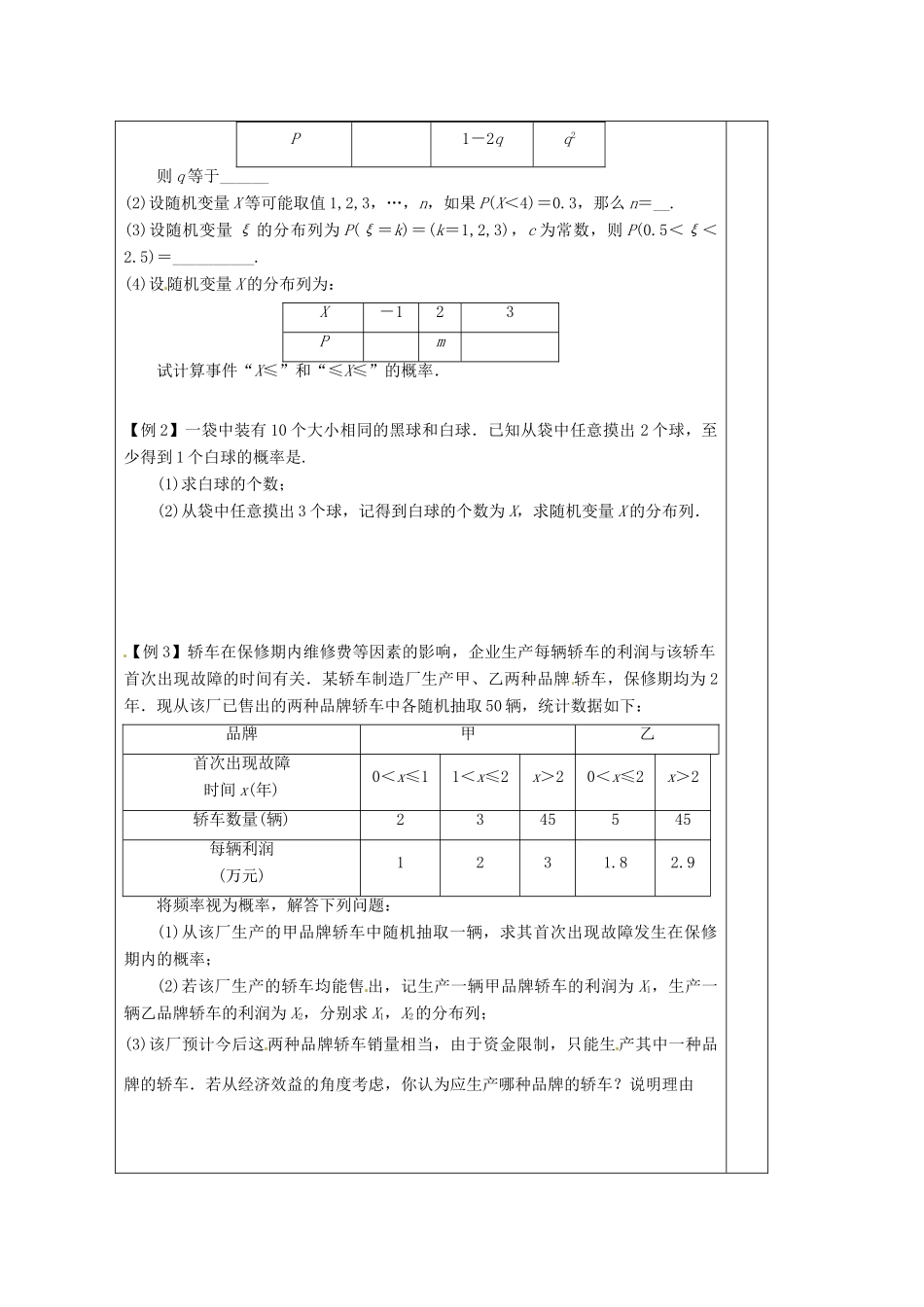
江苏省建陵高级中学 2014 届高考数学二轮复习 专题 22 离散型随机变量及导学案一:学习目标1、 了解取有限值的离散型随机变量及其分布列的概念,了解分布列对于刻画随机现象的重要性;2、 会求某些简单的离散型随机变量的分布列。3、了解超几何分布及其导出过程,并能进行简单的应用。二:课前预习1.随机变量 :在随机试验中,随着________变化而变化的变量称为随机变量.2.离散型随机变量:所有取值可以________的随机变量,称为离散型随机变量.随机变量通常用大写字母 X,Y,Z 等表示,也可以用希腊字母 ξ,η 等表示.3.一般地,若离散型随机变量 X可能取的不同值为 x1,x2,…,xn,X 取每一个值xi(i=1,2,…,n)的概率 P(X=xi)=pi,以表格的形式表示如下:Xx1x2…xi…xnPp1p2…pi…pn此表称为离散型随机变量 X 的__________,简称为 X 的______.有时为了表达简单,也用等式________________表示 X 的分布列.4. 离散型随机变量的分布列具有如下性质:(1)pi≥0 , i = 1,2 , … , n ; (2)________.5.两点分布:若随机变量 X 的分布列为:则称这样的分布列为__________.如果随机变量 X 的分布列为两点分布列,就称 X 服从两点分布.6.超几何分布:在含有 M 件次品的 N 件产品中,任取 n 件,其中恰有 X 件次品,则事件“X=k”发生的概率 P(X=k)=______________,称随机变量 X 服从超几何分布.7.设随机变量 X 的概率分布 P(X=k)=,k=0、1、2、3,则 c=_ __.8.设某项试验的成功率为失败率的 2 倍,用随机变量 X 去描述 1 次试验的成功次数,则 P(X=0)的值为________.9.在一个口袋中装有黑、白两个球,从中随机取一球,记下它的颜色,然后放回,再取一球,又记下它的颜色,写出这两次取出白球数 η 的分布列为__________.三:课堂研讨【例 1】(1)设 X 是一个离散型随机变量,其分布列为:X-101备 注X01P1-ppP1-2qq2则 q 等于______(2)设随机变量 X 等可能取值 1,2,3,…,n,如果 P(X<4)=0.3,那么 n=__.(3)设随机变量 ξ 的分布列为 P(ξ=k)=(k=1,2,3),c 为常数,则 P(0.5<ξ<2.5)=__________.(4)设随机变量 X 的分布列为:X-123Pm试计算事件“X≤”和“≤X≤”的概率.【例 2】一袋中装有 10 个大小相同的黑球和白球.已知从袋中任意摸出 2 个球,至少得到 1 个白球的概率是.(1)求白球的个数;(2)从袋中...