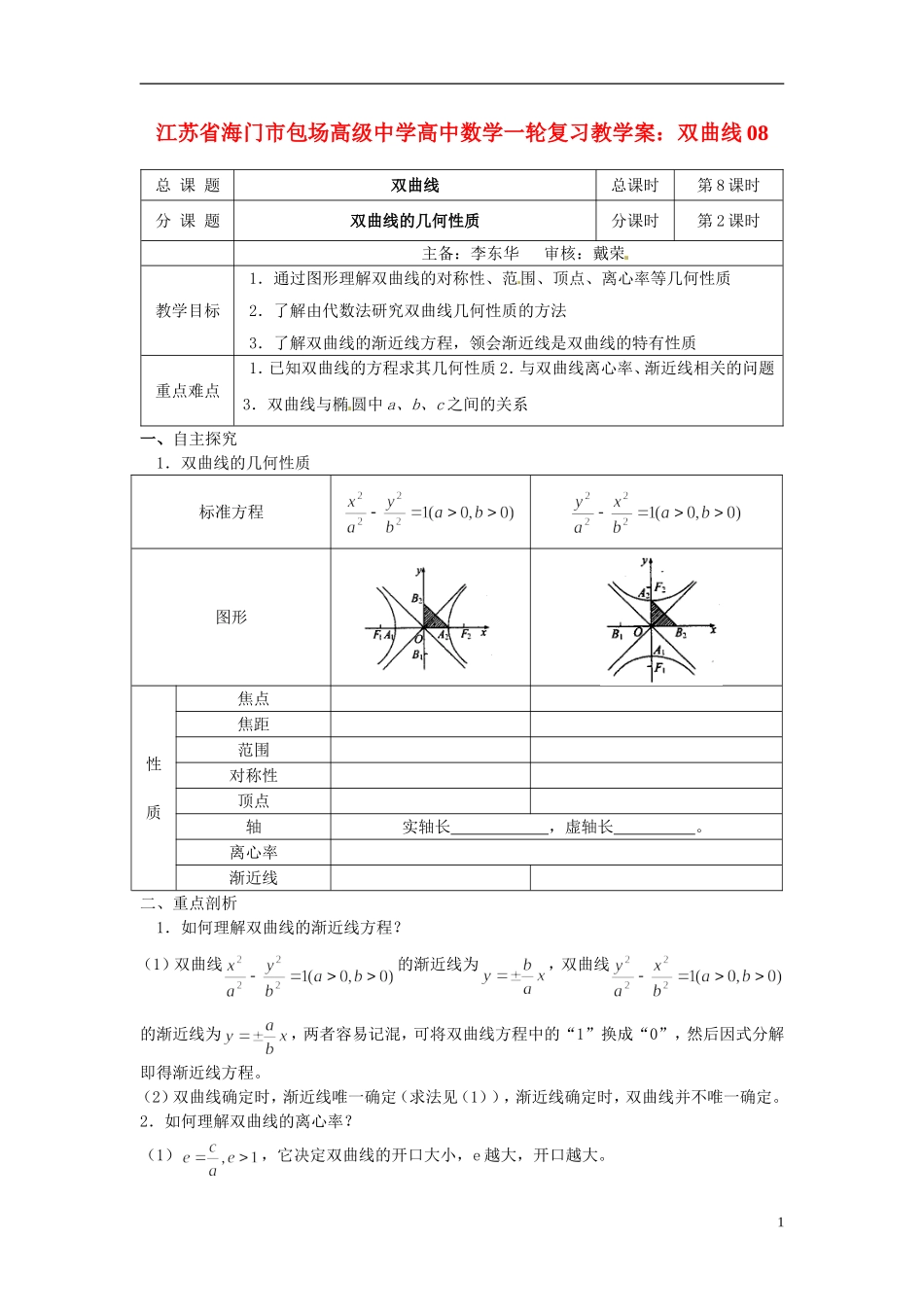
江苏省海门市包场高级中学高中数学一轮复习教学案:双曲线 08总 课 题双曲线总课时第 8 课时分 课 题双曲线的几何性质分课时第 2 课时主备:李东华 审核:戴荣教学目标1.通过图形理解双曲线的对称性、范围、顶点、离心率等几何性质2.了解由代数法研究双曲线几何性质的方法3.了解双曲线的渐近线方程,领会渐近线是双曲线的特有性质重点难点1.已知双曲线的方程求其几何性质 2.与双曲线离心率、渐近线相关的问题3.双曲线与椭圆中 a、b、c 之间的关系一、自主探究 1.双曲线的几何性质标准方程图形性质焦点焦距范围对称性顶点轴实轴长 ,虚轴长 。离心率渐近线二、重点剖析 1.如何理解双曲线的渐近线方程?(1)双曲线的渐近线为,双曲线的渐近线为,两者容易记混,可将双曲线方程中的“1”换成“0”,然后因式分解即得渐近线方程。(2)双曲线确定时,渐近线唯一确定(求法见(1)),渐近线确定时,双曲线并不唯一确定。2.如何理解双曲线的离心率?(1),它决定双曲线的开口大小,e 越大,开口越大。1(2)等轴双曲线的两渐近线互相垂直,离心率 例 2.根据下列条件,求双曲线的标准方程(1)已知双曲线的渐近线方程为,焦距为 10;(2)已知双曲线的渐近线方程为,且过点 M();(3)与椭圆有公共焦点,且离心率【变式训练】焦点在坐标轴上的双曲线,它的两条渐近线方程为,焦点到渐近线的距离为 3,求此双曲线的方程例 3.如图,F1 和 F2 分别是双曲线的两个焦点 ,A、B 是以 O 为圆心、以 OF1为半径的圆与该双曲线左支的两个交点,且△F2AB 是等边三角形,求双曲线的离心率。【变式训练】(1)在平面直角坐标系 xoy 中,双曲线中心在原点,一条渐近线方程为,求双曲线的离心率。(2)设双曲线的两个焦点分别为 F1、F2,点 P 在双曲线上,若,且。求此双曲线的离心率。四、基础达标21.双曲线方程为,则它的右焦点坐标为 。2.若双曲线的渐近线方程为,它的一个焦点是(,0),则双曲线的方程是 。4.双曲线的两条渐近线所成的锐角为 。3.求中心在原点,顶点间距离为 6,渐近线为的双曲线方程。五、归纳小结六、课后作业: 高二 班级 姓名 1、已知双曲线,则 x 的取值范围是 。2、双曲线的渐近线方程为 。3、求适合下列条件的双曲线的标准方程:(1)一个顶点坐标为,焦距为: 。(2)一条渐近线方程为,实轴长为 12: 。(3)顶点在坐标轴上,实轴长为 8,虚轴长为 10 的双曲线的...