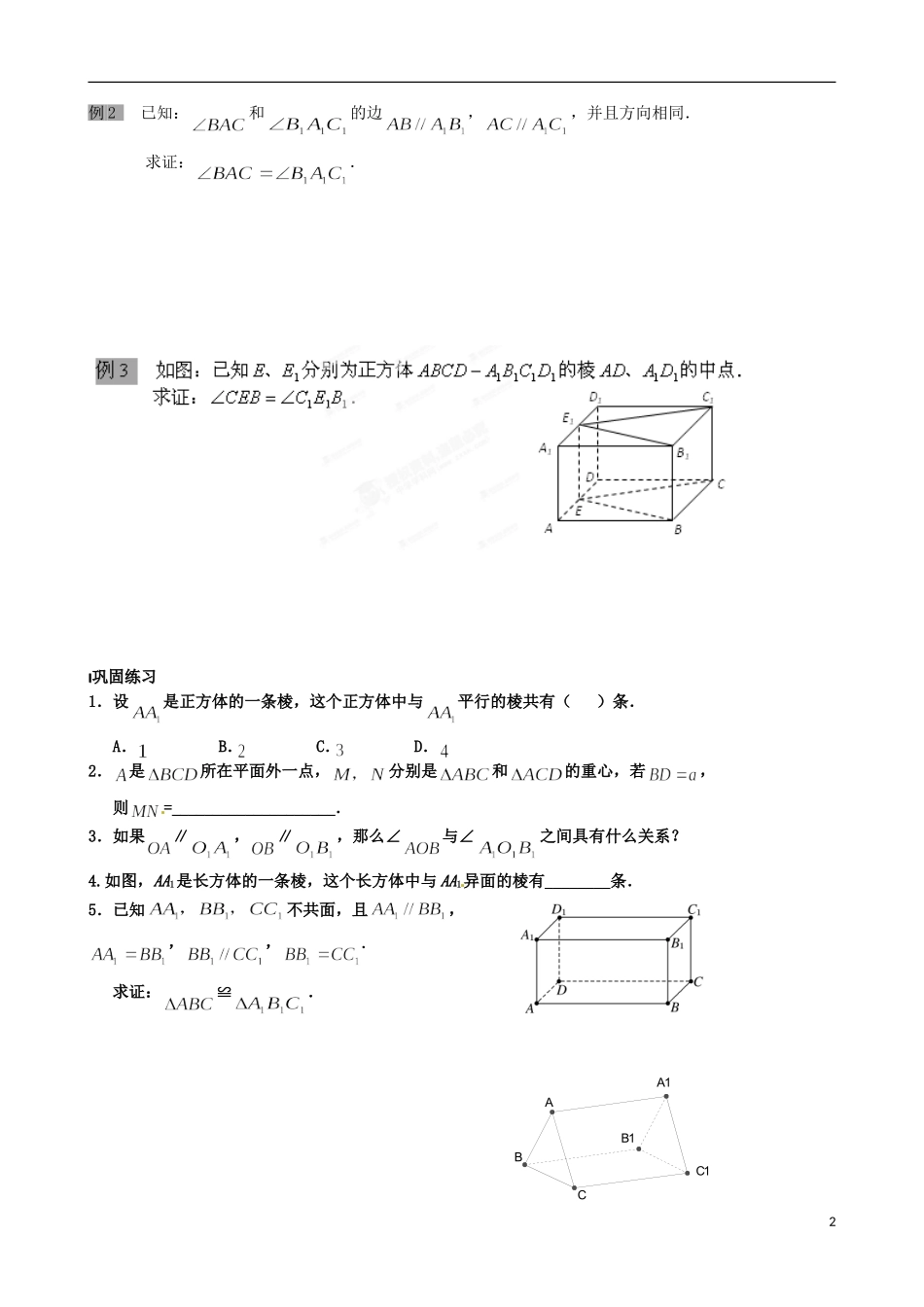
江苏省涟水县第一中学高中数学 空间两直线的位置关系教学案 1 苏教版必修 2总 课 题点、线、面之间的位置关系总课时第 7 课时分 课 题分课时第 1 课时教学目标了解空间中两条直线的位置关系;理解并掌握公理 ;理解并掌握等角定理.重点难点公理 及等角定理.引入新课引入新课1.问题 1:在平面几何中,两直线的位置关系如何?问题 2:没有公共点的直线一定平行吗?问题 3:没有公共点的两直线一定在同一平面内吗?2.异面直线的概念:________________________________________________________________________.3.空间两直线的位置关系有哪几种?位置关系共面情况公共点个数4.公理 4:(文字语言)_______________________________________.(符号语言)_________________________________________.5.等角定理:________________________________________.例题剖析例题剖析例 1 如图,在长方体中,已知分别是的中点.求证:.1ABEFCDA1D1C1B1例 2 已知:和的边,,并且方向相同.求证:.巩固练习巩固练习1.设是正方体的一条棱,这个正方体中与平行的棱共有( )条.A.B.C.D.2.是所在平面外一点,分别是和的重心,若,则=____________________.3.如果∥,∥,那么∠与∠之间具有什么关系?4.如图,AA1是长方体的一条棱,这个长方体中与 AA1异面的棱有________条.5.已知不共面,且,,,.求证:≌.2B1AA1BCC1课堂小结课堂小结了解空间中两条直线的位置关系;理解并掌握公理 ;理解并掌握等角定理.3课后训练课后训练班级:高二( )班 姓名:____________一 基础题1.若把两条平行直线称为一对,则在正方体条棱中,相互平行的直线共有_______对.2.已知∥,,,则等于_______________.3.空间三条直线,若,则由直线确定______个平面.4.若平面 α∩β=l,aα,bβ,则 a,b 的位置关系是________.二 提高题5.如图,在三棱锥中,分别是边的中点.(1)求证:四边形是平行四边形;(2)若,求证:四边形为菱形;(3)当与满足什么条件时,四边形是正方形? 6.已知分别是空间四边形四条边上的点.且,分别为的中点,求证:四边形是梯形.4BFCGDHEA三 能力题7.在正方体中,,求证:∥.5ABCDA1D1C1B1EF E1F1