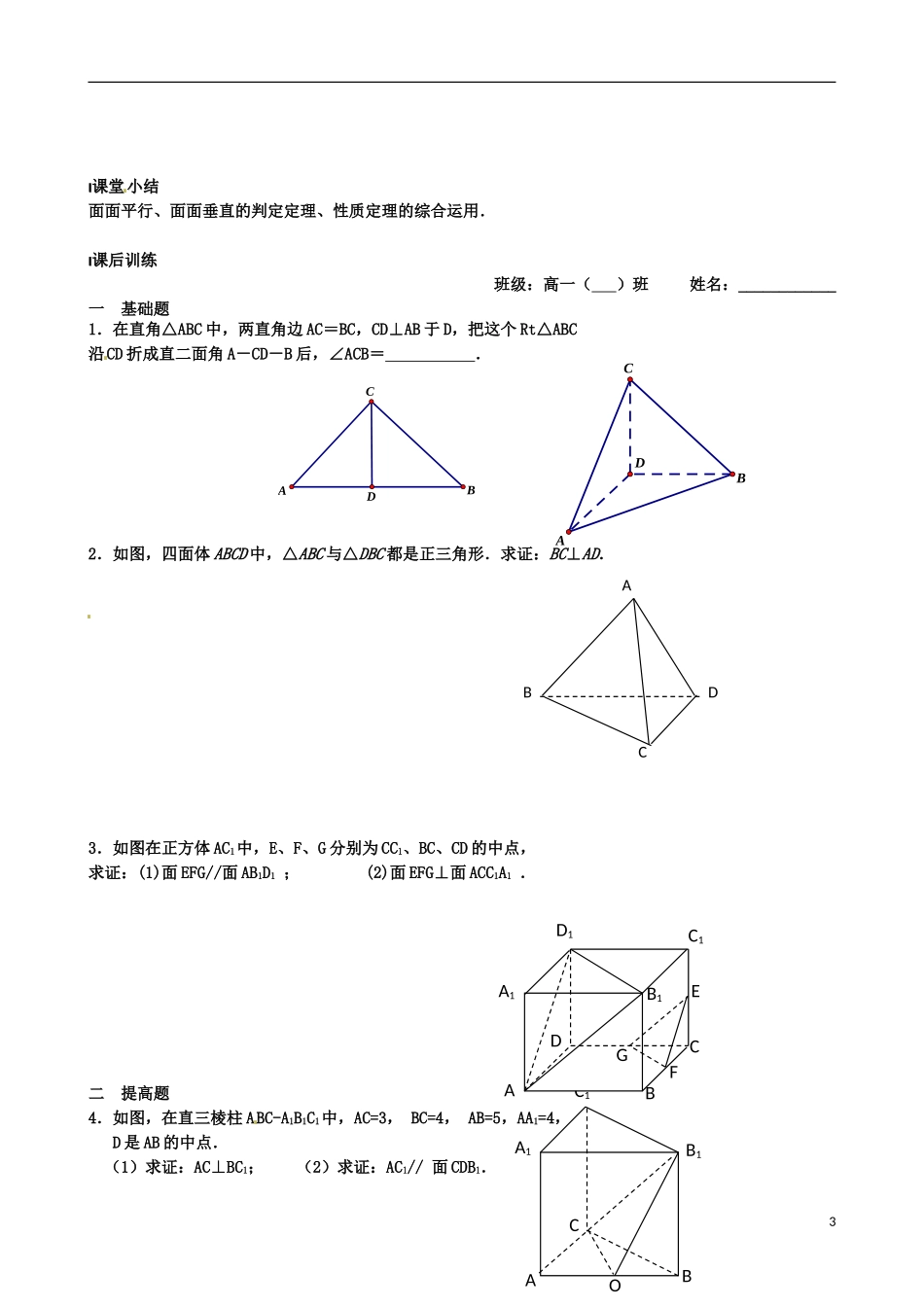
ABCDEFP平面与平面的位置关系综合运用总 课 题平面与平面的位置关系总课时第 14 课时分 课 题平面与平面的位置关系综合运用分课时第 3 课时教学目标能综合运用两个平面平行的判定定理和性质定理及 两个平面垂直的判定定理和性质定理解决有关问题.重点难点面面平行、面面垂直的判定定理、性质定理的综合运用.引入新课引入新课1.回顾两个平面平行的判定定理和性质定理:(1)两平面平行的判定定理:符号语言: 图形语言:(2)两平面平行的性质定理:如果两个平面同时和第三个平面相交,那么所得的两条交线平行. 2.回顾两个平面垂直的判定定理和性质定理:(1)两平面垂直的判定定理: 如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直. 符号语言: 图形语言:(2)两平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面. 符号语言: 图形语言:例题剖析例题剖析例 1 如图 ABCD 是边长为的正方形,E,F 分别为 AD,AB 的中点,PC 平面 ABCD,PC=3, (1) 求二面角 P-EF-C 的正切值; (2) 在 PC 上确定一点 M,使平面 MBD//平面 PEF,并说明理由.1AabllaA例 2 如图,在正三棱柱中,点在边上,.(1)求证:平面;(2)如果点是的中点,求证:平面.巩固练习巩固练习1.已知二面角 α-AB-β 的平面角为 θ,α 内一点 C 到 β 的距离为 3,到棱 AB 的距离为 4,则 tanθ=____________________.2.下列命题:① 若直线 a//平面,平面⊥平面 β,则 a⊥β;② 平面⊥平面 β,平面 β⊥平面 γ,则⊥γ;③ 直线 a⊥平面,平面⊥平面 β,则 a//β; ④ 平面//平面 β,直线 a平面,则 a//β.其中正确命题是_________________.④3. (2011 江苏)如图,在四棱锥中,平面平面,分别是的中点.求证:(1)直线平面;(2)平面平面.21AABCDE1B1CABC课堂课堂 小结小结面面平行、面面垂直的判定定理、性质定理的综合运用.课后训练课后训练班级:高一( )班 姓名:____________一 基础题1.在直角△ABC 中,两直角边 AC=BC,CD⊥AB 于 D,把这个 Rt△ABC沿CD 折成直二面角 A-CD-B 后,∠ACB= .2.如图,四面体 ABCD 中,△ABC 与△DBC 都是正三角形.求证:BC⊥AD. 3.如图在正方体 AC1中,E、F、G 分别为 CC1、BC、CD 的中点,求证:(1)面 EFG//面...