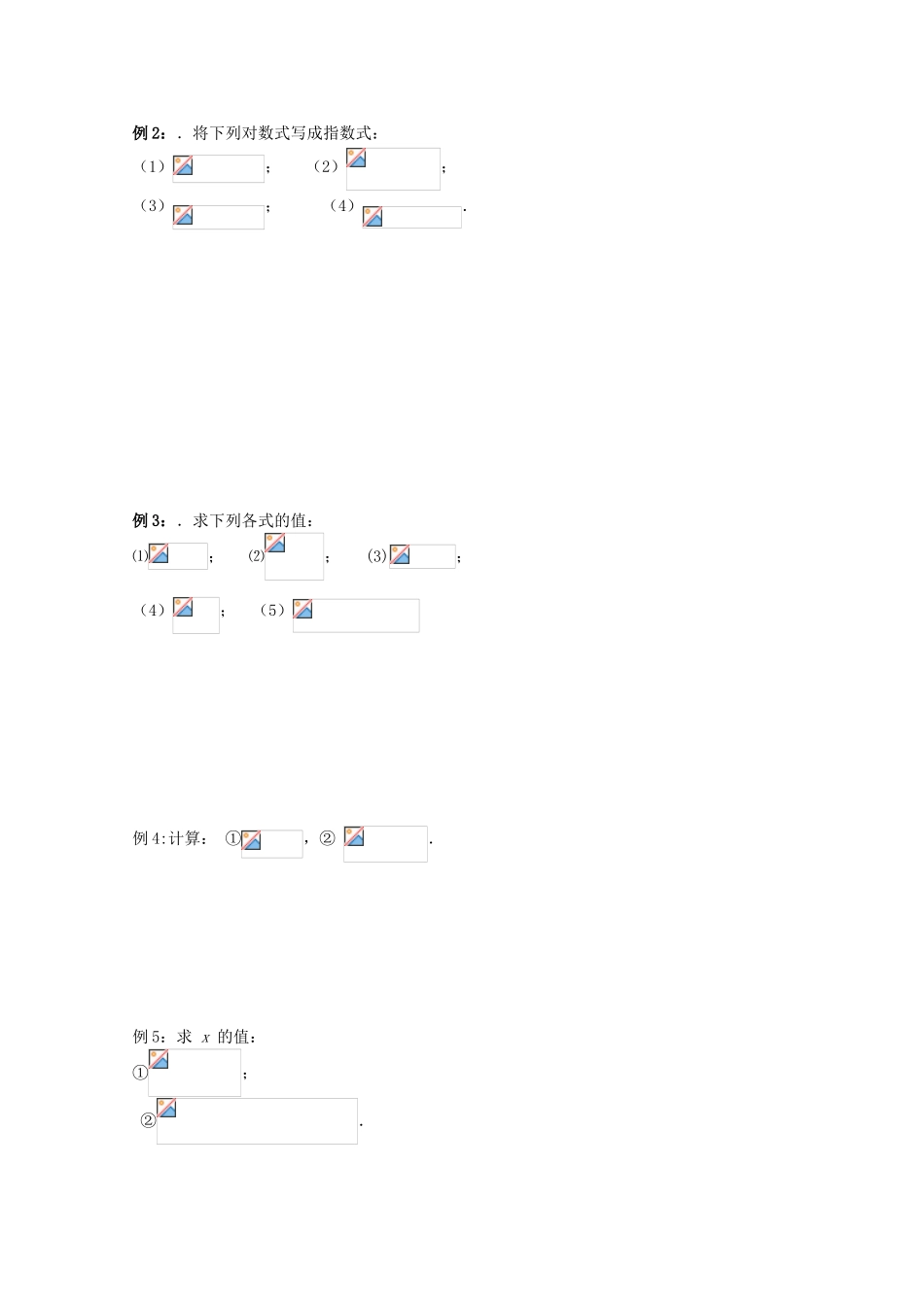
赣马高级中学 2010 级高一数学 对数 (1)导学案 【学习导航】 知识网络 学习要求:1. 理解对数的概念;2. 能够进行对数式与指数式的互化;3.会根据对数的概念求一些特殊的对数式的值。【新课导学】 一、课前准备(预习教材 P62~ P64,找出疑惑之处)复习 1:庄子:一尺之棰,日取其半,万世不竭.(1)取 4 次,还有多长?(2)取多少次,还有 0.125 尺? 复习 2:假设 2002 年我国国民生产总值为 a 亿元,如果每年平均增长 8%,那么经过多少年国民生产 是 2002 年的 2 倍? (只列式)二、新课导学※ 学习探究探究任务:对数的概念问题:截止到 1999 年底,我国人口约 13 亿. 如果今后能将人口年平均增长率控制在1%,那么多少年后人口数可达到 18 亿,20 亿,30 亿?底数真数对数对数对数的定义对数与指数的关系关系有关概念对数函数及性质对数的运算性质讨论:(1)问题具有怎样的共性?(2)已知底数和幂的值,求指数 怎样求呢?例如:由,求 x.新知:一般地,如果,那么数 x 叫做以 a 为底 N 的对数(logarithm).记作 ,其中 a 叫做对数的底数,N 叫做真数 试试:将复习 2 及问题中的指数式化为对数式.新知:我们通常将以 10 为底的对数叫做常用对数(common logarithm),并把常用对数简记为 lgN 在科学技术中常使用以无理数 e=2.71828……为底的对数,以 e 为底的对数叫自然对数,并把自然对数简记作 lnN 试试:分别说说 lg5 、lg3.5、ln10、ln3 的意义.反思:(1)指数与对数间的关系? 时, .(2)负数与零是否有对数?为什么? (3) , .【互动探究】例 1:将下列指数式写成对数式:(1); (2); (3); (4).例 2:.将下列对数式写成指数式:(1); (2); (3); (4).例 3:.求下列各式的值:⑴; ⑵; (3);(4); (5)例 4:计算: ①,② .例 5:求 x 的值:①; ②.③【迁移应用】1.将化为对数式2.将化为指数式3.求值:(1) (2)4 求下列各式中的 x 的值:⑴logx9=2; ⑵lgx2= -2;⑶log2[log2(log2x)]=0(4); (5); (6); (7).答案1. 对数定义:一般地,如果()的次幂等于, 即 ,那么就称是以为底的 对 数 ( logarithm ) , 记 作 , 其 中 ,叫 做 对 数 的 底 数 (base of logarithm) , 叫做真数 (proper number) 。 着重理解对数式与指数式之间的相...