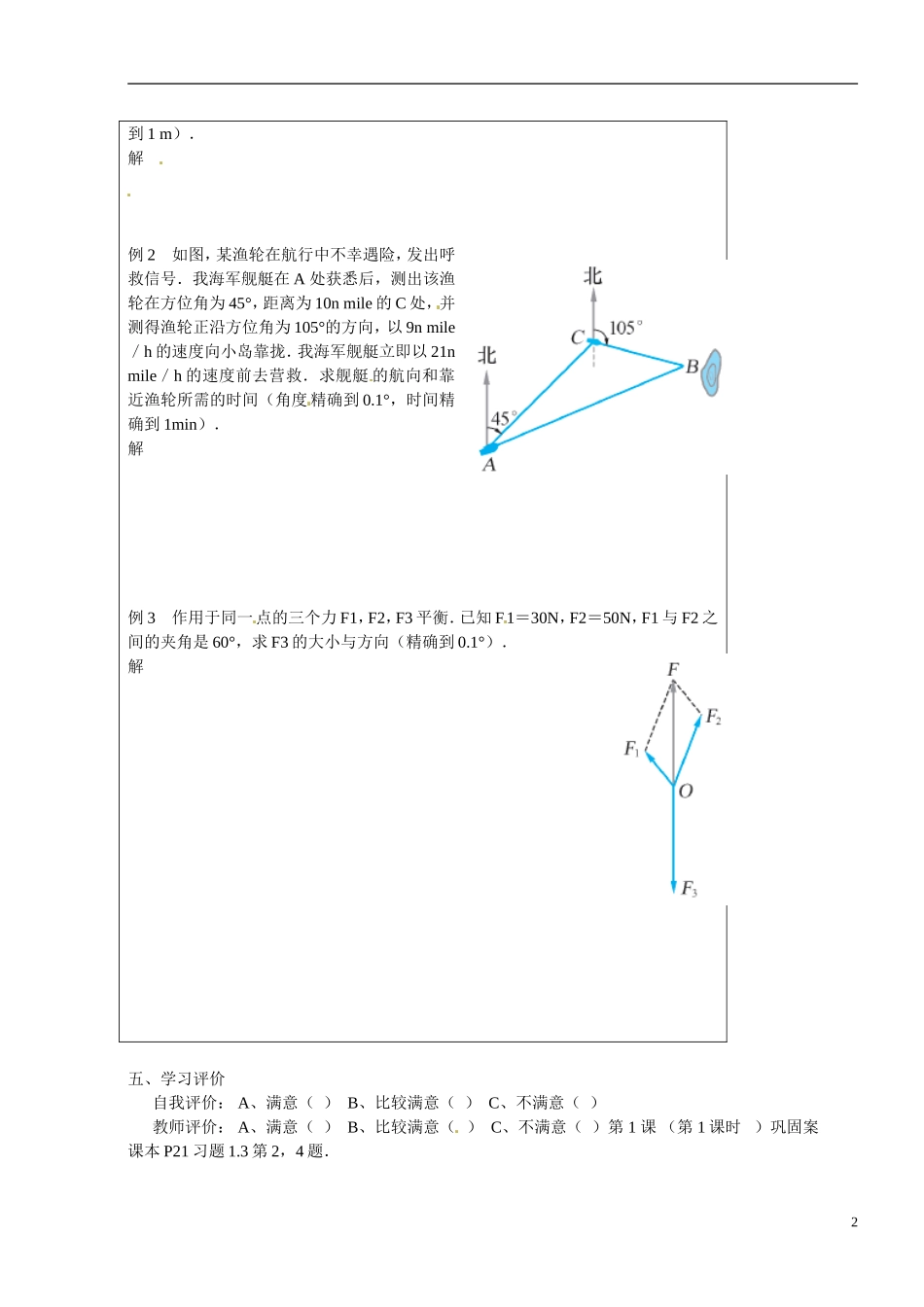
江苏省灌云县陡沟中学高中数学 正弦定理、余弦定理的应用 5 导学案 新人教A 版必修 5 一、学习目标:1.能熟练应用正弦、余弦定理及相关公式解决三 角形中的有关问题;2.能把一些简单的实际问题转化为数学问题,并能应用正弦、余弦定理及相关的三角公式解决这些问题;3.通过复习、小结,使学生牢固掌握两个定理,应用自如.二、学习重点:能熟练应用正弦、余弦定理及相关公式解决三角形的有关问题,牢固掌握两个定理,应用自如.三、学习难点:能熟练应用正弦、余弦定理及相关公式解决三角形的有关问题,牢固掌握两个定理,应用自如.四、学习过程(根据学科特点选择性灵活运用)●自主质疑一、复习:正弦定理、余弦定理及其变形形式,解斜三角形的要求和常用方法.1.正弦定理、三角形面积公式:RCcBbAa2sinsinsin;BacCabAbcS ABCsin21sin21sin21.2.正弦定理的变形:(1)CRcBRbARasin2,sin2,sin2;(2)RcCRbBRaA2sin,2sin,2sin;(3)sinsinsin::: :ABCa b c.3.利用正弦定理和三角形内角和定理,可以解决以下两类解斜三角形问题:(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角,从而进一步求其它的边和角.4.余弦定理:bcacbAAbccba2cos,cos2222222.5.应用余弦定理解以下两类三角形问题:(1)已知三边求三内角;(2)已知两边和它们的夹角,求第三边和其他两个内角.●合作探究例 1 如图,为了测量河对岸两点 A,B 之间的距离,在河岸这边取点 C,D,测得∠ADC=85°,∠BDC=60°,∠ACD=47°,∠BCD=72°,CD=100m.设A,B,C,D 在同一平面内,试求 A,B 之间的距离(精确1到 1 m).解 例 2 如图,某渔轮在航行中不幸遇险,发出呼救信号.我海军舰艇在 A 处获悉后,测出该渔轮在方位角为 45°,距离为 10n mile 的 C 处,并测得渔轮正沿方位角为 105°的方向,以 9n mile/h 的速度向小岛靠拢.我海军舰艇立即以 21n mile/h 的速度前去营救.求舰艇 的航向和靠近渔轮所需的时间(角度 精确到 0.1°,时间精确到 1min).解 例 3 作用于同一点的三个力 F1,F2,F3 平衡.已知 F1=30N,F2=50N,F1 与 F2 之间的夹角是 60°,求 F3 的大小与方向(精确到 0.1°).解五、学习评价 自我评价: A、满意( ) B、比较满意( ) C、不满意( ) 教师评价: A、满意( ) B、比较满意( ) C、不满意( )第 1 课 (第 1 课时 )巩固案课本 P21 习题 1.3 第 2,4 题.2