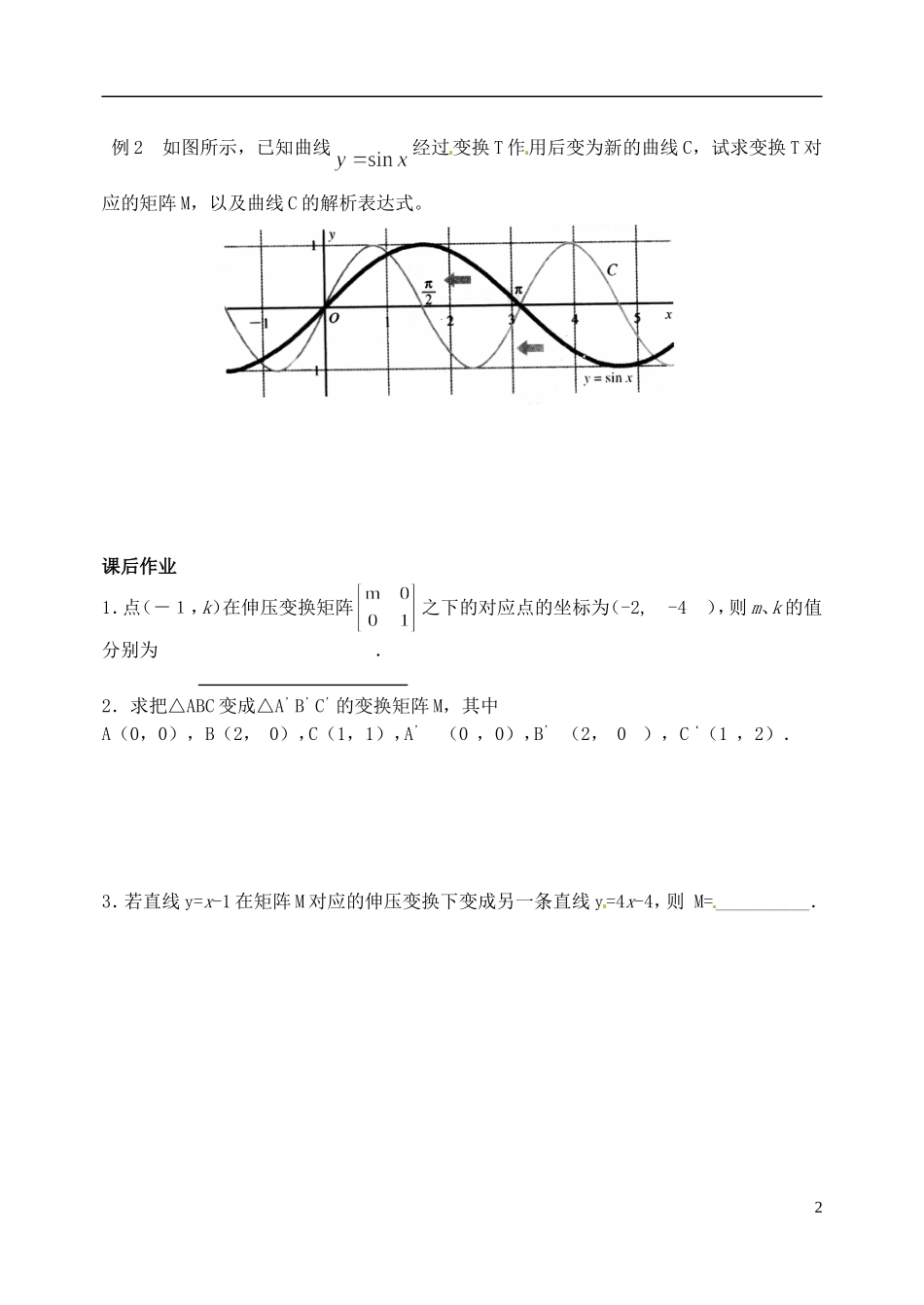
江苏省西亭高级中学高中数学选修 4-2《恒等变换与伸压变换》学案学习目标1.理解可以用矩阵来表示平面中常见的几何变换.2.掌握恒等、伸压变换的几何意义及其矩阵表示.课前导学1.________________________称为恒等变换,这时称矩阵 M 为__________________,二阶单位矩阵一般记为 E,平面上任何一点(向量)或图形,在恒等变换之下都把自己变为自己.2._________________________称为 (垂直)伸压变换,这时称矩阵 M =___________或 M = ____________伸压变换矩阵.3.当 k 1 时,伸压变换 M =确定的变换,将原来平面图形上的横坐标_________,纵坐标__________;当 0 < k < 1 时,伸压变换 M =确定的变换,将原来平面图形上的横坐标_____________,纵坐标__________.4.当 k 1 时,伸压变换M =确定的变换,将原来平面图形上的横坐标________,纵坐标_________________;当 0 < k < 1 时,伸压变换 M =确定的变换,将原来平面图形上的横坐标_________,纵坐标________________________.5.在伸压变换之下,直线仍然变为_________,线段仍然变为___________.6.恒等变换是_______________的特例,伸压变换多与三角函数图象的变换联系起来研究.课堂探究例 1 求 在矩阵 M= 作用下的图形. 变题:将矩阵 M 变为,结果如何?1例 2 如图所示,已知曲线经过变换 T 作用后变为新的曲线 C,试求变换 T 对应的矩阵 M,以及曲线 C 的解析表达式。课后作业1.点(-1,k)在伸压变换矩阵之下的对应点的坐标为(-2, -4 ),则 m、k 的值分别为 .2.求把△ABC 变成△A’B’C’的变换矩阵 M,其中A(0,0),B(2, 0),C(1,1),A’(0 ,0),B’ (2, 0),C‘(1 ,2).3.若直线 y=x-1 在矩阵 M 对应的伸压变换下变成另一条直线 y=4x-4,则 M=__________.2