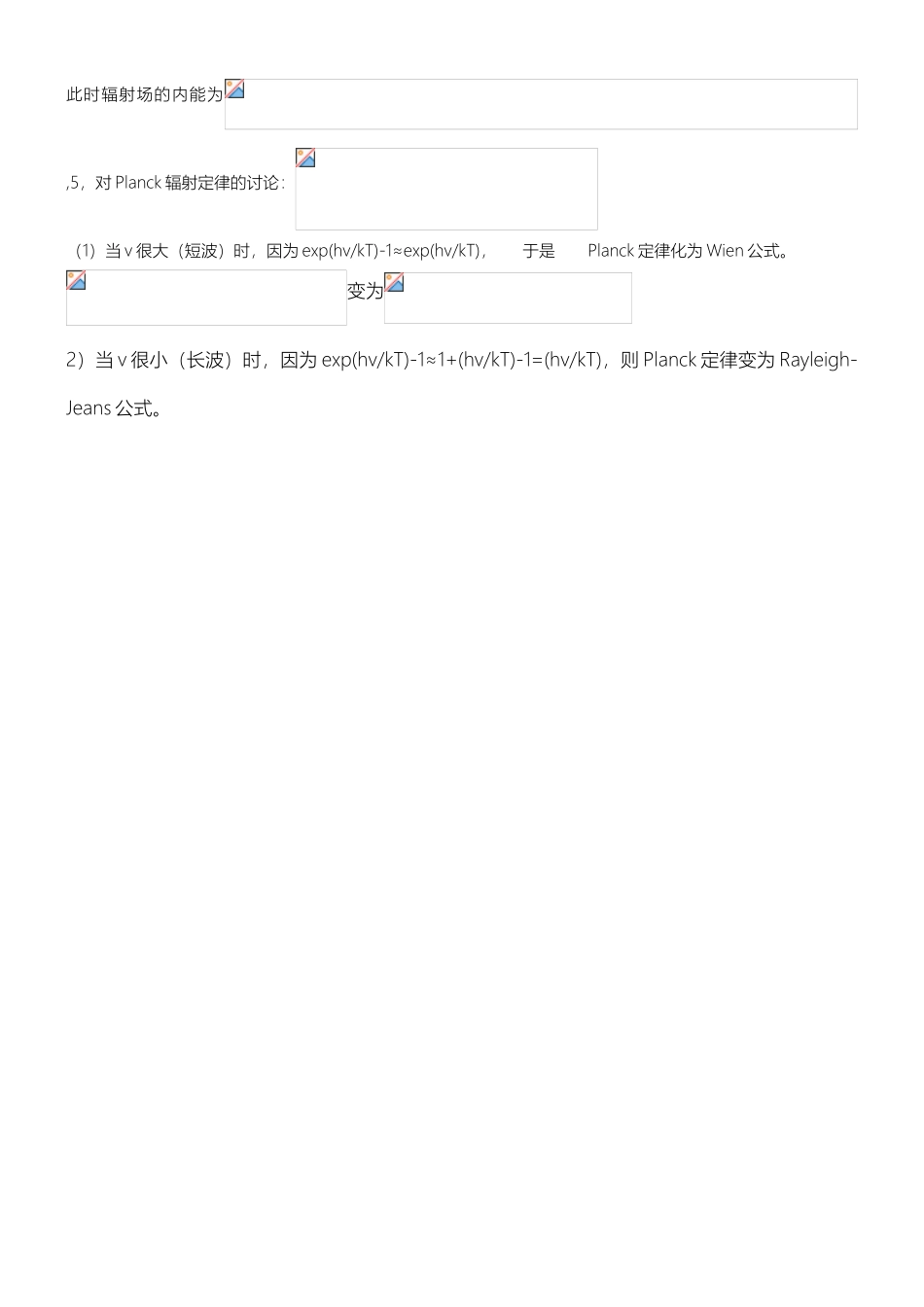
普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。辐射热平衡状态:处于某一温度 T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度 T 有关而与黑体的形状和材料无关。实验得到:1.Wien 公式从热力学出发加上一些特别的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在 高 频 区 公 式 与 实 验 不 符 , 并 且,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是,该式 叫 做 Stefan-Bolzmann 公 式 ,叫 做Stefan-Bolzmann 常数。3. Planck 黑体辐射定律1900 年12月14日 Planck 提出假如空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率 v 振荡;(2)黑体只能以 E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。得到:该式称为 Planck 辐射定律h 为普朗克常数,h=4,普朗克的推导过程:把 空 窖 内 的 电 磁 波 分 解 为 各 个 频 率 的 简 振 振 动 , 简 振 模 的 形 式 最 后 为,每一个简振模在力学上等价于一个自由度,记频率在内的自由度数为,则(0,v)范围内的总自由度数 G(v)与 g(v)的关系为。借助几何方法求出,取微分得令代表体积为 V 的空窖内热平衡辐射的总内能,代表单位体积,频率间隔在内的能量,于是,,代表单位体积内频率间隔在内的振动自由度数。应用经典统计的能量均分定理得到平均能量为与振子的频率无关,代入可以得到,这就是瑞利-金斯公式,在低频区和实验符合,高频区严重偏离。普朗克热辐射理论采纳的也是波的观点,依旧认为他正确,但是能量均分定理不适用,原因在于麦克斯韦——波尔滋蔓分布不对,问题出在振子能量取连续值上。Planck 假定:黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量,对...