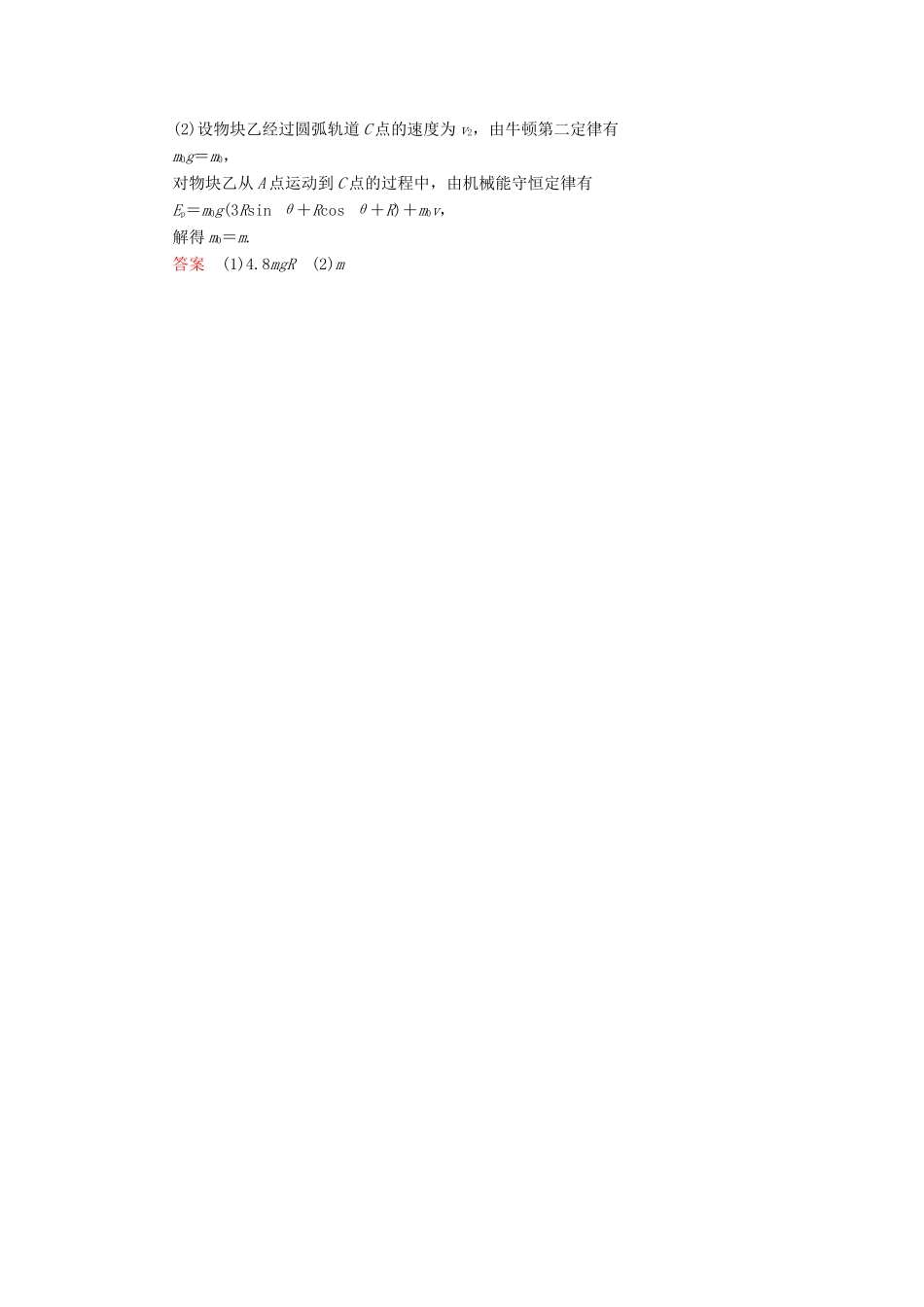
第16讲机械能守恒定律及其应用1.如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,且处于原长状态.现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中(B)A.圆环的机械能守恒B.弹簧弹性势能变化了mgLC圆环下滑到最大距离时,所受合力为零D.圆环重力势能与弹簧弹性势能之和保持不变解析圆环沿杆下滑的过程中,圆环与弹簧组成的系统动能、弹性势能、重力势能之和守恒,选项A、D错误;弹簧长度为2L时,圆环下落的高度h=L,根据机械能守恒定律,弹簧的弹性势能增加了ΔEp=mgh=mgL,选项B正确;圆环释放后,圆环向下先做加速运动,后做减速运动,当速度最大时,合力为零,下滑到最大距离时,具有向上的加速度,合力不为零,选项C错误.2.(多选)如图,滑块a、b的质量均为m,a套在固定竖直杆上,与光滑水平地面相距h,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点,重力加速度大小为g.则(BD)A.a落地前,轻杆对b一直做正功B.a落地时速度大小为C.a下落过程中,其加速度大小始终不大于gD.a落地前,当a的机械能最小时,b对地面的压力大小为mg解析设某一时刻a、b速度分别为va、vb,则vacosθ=vbsinθ.当a落到地面时,θ=90°,cosθ=0,故vb为0,可知a下落过程中b先加速后减速,轻杆对b先做正功后做负功,选项A错误.轻杆对a的力先为支持力后为拉力,故a的加速度先小于g后大于g,选项C错误.由于a、b系统只有重力和系统内杆的弹力做功,故a、b机械能守恒,a落地时b速度为零,由机械能守恒定律得mgh=mv,得va=.选项B正确.当a机械能最小时,b的机械能最大,即动能最大,此时F杆=0,故FN=mg,选项D正确.3.如图,在竖直平面内有由圆弧AB和圆弧BC组成的光滑固定轨道,两者在最低点B平滑连接.AB弧的半径为R,BC弧的半径为.一小球在A点正上方与A相距处由静止开始自由下落,经A点沿圆弧轨道运动.(1)求小球在B、A两点的动能的比值;(2)通过计算判断小球能否沿轨道运动到C点.解析(1)设小球的质量为m,小球在A点的动能为EkA,由机械能守恒得EkA=mg,①设小球在B点的动能为EkB,同理有EkB=mg,②由①②式得=5.③(2)若小球能沿轨道运动到C点,小球在C点所受轨道的正压力N应满足N≥0,④N+mg=m,⑤由④⑤式得,vC应满足mg≤m,⑥由机械能守恒有mg=mv,⑦由⑥⑦式可知,小球恰好可以沿轨道运动到C点.答案(1)5(2)能4.如图所示,倾角θ=37°光滑斜面的底端的固定挡板上连接一轻弹簧,斜面顶端与半径为R的竖直平面内的光滑圆弧轨道相切于B点.质量m的物块甲将弹簧压缩至A点,A、B间距为3R,由静止释放物块甲,物块甲运动到圆弧轨道最高点C时,对轨道的压力大小等于物块甲重力的1.4倍,不计空气阻力,重力加速度为g,sin37°=0.6,cos37°=0.8.(1)求释放物块甲时弹簧具有的弹性势能Ep;(2)若将物块甲换成物块乙,仍将弹簧压缩至A点后由静止释放,为使物块乙恰能经过圆弧轨道最高点C,求物块乙的质量m0.解析(1)根据牛顿第三定律可得,物块甲经过圆弧轨道C点,轨道对物块甲的弹力为1.4mg,设物块甲经过圆弧轨道C点的速度为v1,由牛顿第二定律有1.4mg+mg=m,对物块甲从A点运动到C点的过程中,由机械能守恒定律有Ep=mg(3Rsinθ+Rcosθ+R)+mv,解得Ep=4.8mgR.(2)设物块乙经过圆弧轨道C点的速度为v2,由牛顿第二定律有m0g=m0,对物块乙从A点运动到C点的过程中,由机械能守恒定律有Ep=m0g(3Rsinθ+Rcosθ+R)+m0v,解得m0=m.答案(1)4.8mgR(2)m