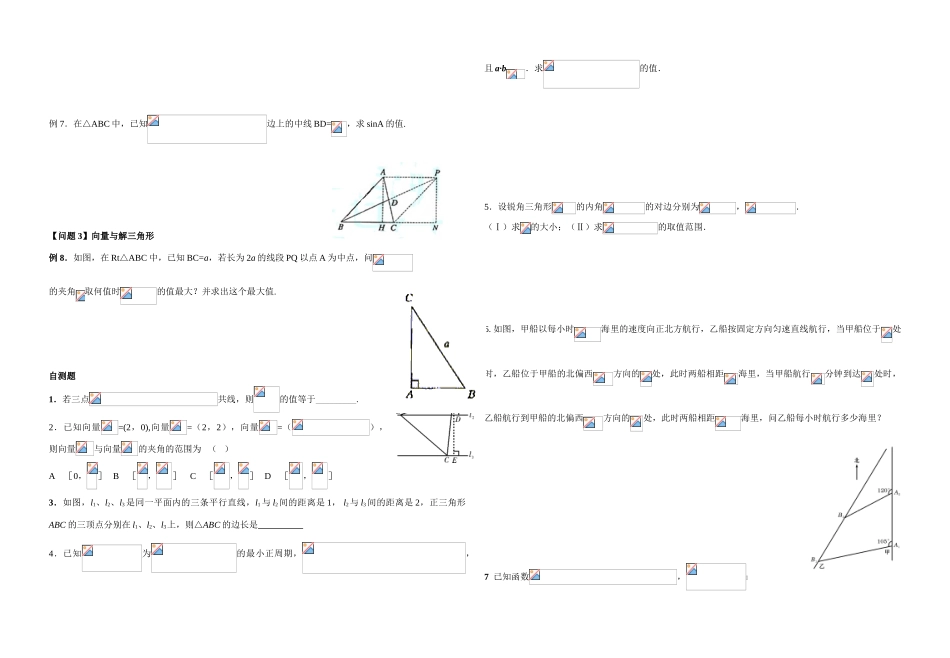
江苏赣榆县赣马高级中学高三数学期末复习教学案 04平面向量内 容要 求ABC5.平面向量平面向量的有关概念√平面向量的线性运算√平面向量的坐标表示√平面向量的的数量积√平面向量的平行与垂直√平面向量的应用√4.解三角形正弦定理、余弦定理及其应用√一、平面向量的概念和性质考点 1:向量的概念、向量的加法和减法、实数与向量的积.考点 2:向量的坐标运算、平面向量的数量积. 考点 3:向量的模与角的计算。.【考型 1】向量的有关概念与运算例 1:已知 a 是以点 A(3,-1)为起点,且与向量 b = (-3,4)平行的单位向量,则向量 a 的终点坐标是 例 2:已知| a |=1,| b |=1,a 与 b 的夹角为 60°, x =2a-b,y=3b-a,则 x 与 y 的夹角的余弦是 【考型 2】向量共线与垂直条件的考查例 3.已知平面向量 a=(,-1),b=(, ).(1) 若存在实数 k 和 t,便得 x=a+(t2-3)b, y=-ka+tb,且 x⊥y,试求函数的关系式 k=f(t);(2) 根据(1)的结论,确定 k=f(t)的单调区间.例 4:已知向量,若正数 k 和 t 使得向量垂直,求 k 的最小值.二、解三角形考点 1:正弦定理、余弦定理、勾股定理考点 2:面积公式、内角和定理【问题 1】三角形内角和定理的灵活运用例 5.已知锐角三角形 ABC 中,(Ⅰ)求证:; (Ⅱ)设 AB=3,求 AB 边上的高.【问题 2】正弦定理、余弦定理、面积公式的灵活应用例 6:在△ABC 中,已知,求△ABC 的面积.例 7.在△ABC 中,已知边上的中线 BD=,求 sinA 的值.【问题 3】向量与解三角形例 8.如图,在 Rt△ABC 中,已知 BC=a,若长为 2a 的线段 PQ 以点 A 为中点,问的夹角取何值时的值最大?并求出这个最大值.自测题1.若三点共线,则的值等于_________.2.已知向量=(2,0),向量=(2,2),向量=(),则向量与向量的夹角的范围为 ( )A [0,] B [,] C [,] D [,]3.如图,l1、l2、l3是同一平面内的三条平行直线,l1与 l2间的距离是 1, l2与 l3间的距离是 2,正三角形ABC 的三顶点分别在 l1、l2、l3上,则△ABC 的边长是 4.已知为的最小正周期,,且 a·b.求的值.5.设锐角三角形的内角的对边分别为,.(Ⅰ)求的大小;(Ⅱ)求的取值范围.6. 如图,甲船以每小时海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于处时,乙船位于甲船的北偏西方向的处,此时两船相距海里,当甲船航...