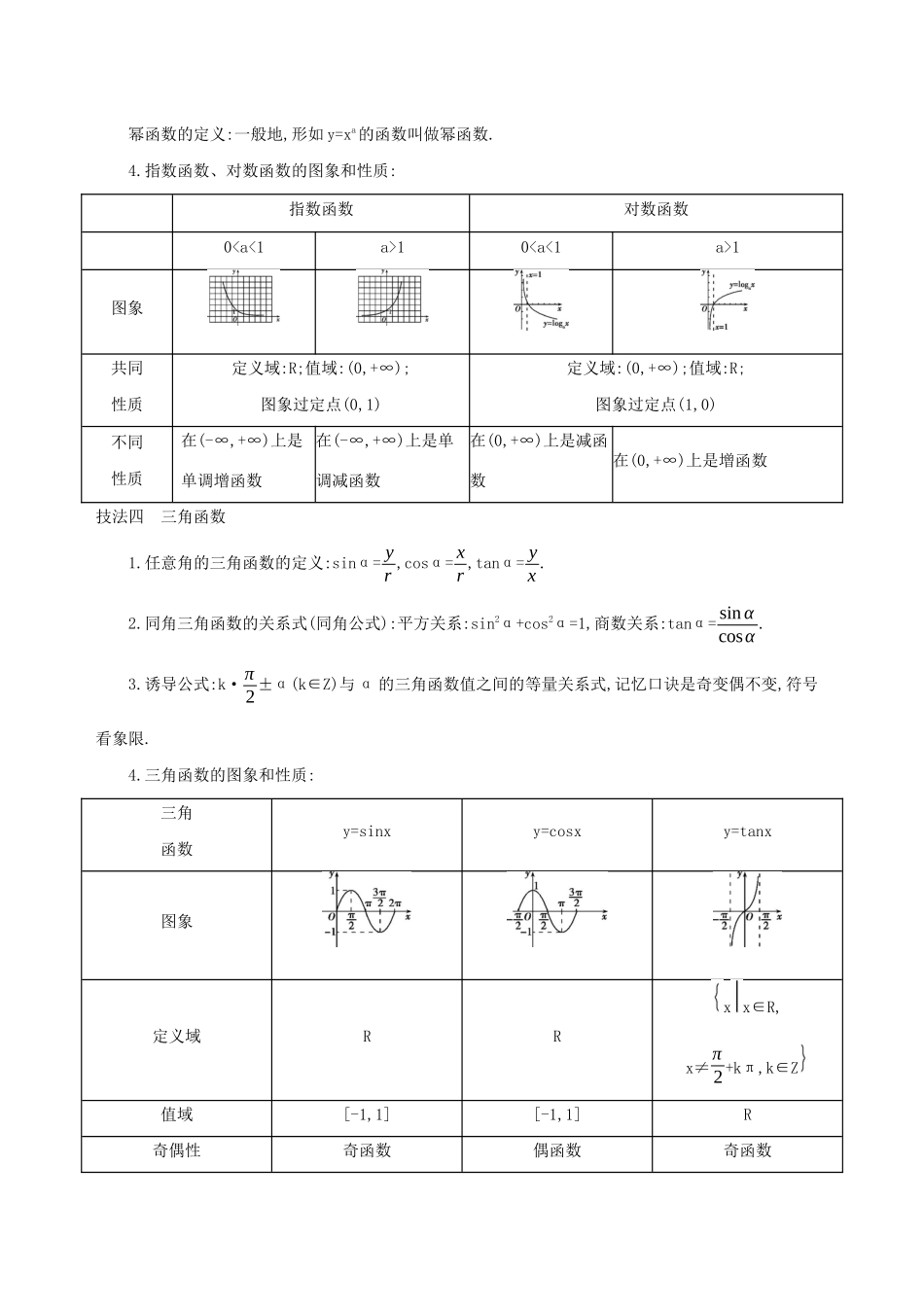
必备一 主干知识回扣技法一 函数性质 1.函数的单调性(1)定义:一般地,设函数 f(x)的定义域为 A,如果对于属于定义域 A 内某个区间 I 上的任意两个自变量的值 x1,x2,当 x1f(x2)),那么就说 f(x)在这个区间 I 上是增(减)函数.(2)证明方法:定义法、导数法.2.函数的奇偶性(1)定义:对于函数 f(x),如果对于定义域内任意一个 x 都有 f(-x)=-f(x),那么 f(x)就叫做奇函数;如果对于定义域内任意一个 x 都有 f(-x)=f(x),那么 f(x)就叫做偶函数.如果函数 f(x)是奇函数或偶函数,那么就说函数 f(x)具有奇偶性.(2)图象特征:奇函数的图象关于原点对称;偶函数的图象关于 y 轴对称.3.函数零点(1)对于函数 y=f(x),x∈D,我们把使函数 y=f(x)的值为 0 的实数 x(x∈D)称为函数 y=f(x)的零点,实质上函数 y=f(x)的零点就是方程 f(x)=0 的根,它是实数而不是点.函数 y=f(x)-g(x)的零点可以看成是方程 f(x)-g(x)=0 的根或函数 y=f(x)的图象与函数 y=g(x)的图象的交点的横坐标.(2)零点存在性定理:一般地,若函数 y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且f(a)·f(b)<0,则函数 y=f(x)在区间(a,b)上有零点.这一定理一般用来证明函数有零点,其逆命题是假命题.技法二 导数 1.导数的几何意义:f'(x0)表示曲线 f(x)在点 P(x0,f(x0))处的切线斜率.2.常见的导数公式:(xn)'=nxn-1;(ax)'=axlna(a>0 且 a≠1);(ex)'=ex;(logax)'=1xln a (a>0 且 a≠1);(lnx)'=1x;(sinx)'=cosx;(cosx)'=-sinx.3.导数的运算法则:[f(x)±g(x)]'=f'(x)±g'(x);[f(x)·g(x)]'=f'(x)·g(x)+f(x)·g'(x);[f ( x)g( x )]'=f '( x) g( x )-f ( x ) g'( x )[ g( x )]2(g(x)≠0).4.导数与函数的单调性:f'(x)>0⇒函数 f(x)在相应区间上为单调增函数;f'(x)<0⇒函数 f(x)在相应区间上为单调减函数.5.导数与函数的极值、最值:(1)函数的极值:设函数 f(x)在点 x0附近有定义,且对 x0附近的所有点都有 f(x)f(x0),则称 f(x0)为函数 f(x)的一个极大(或小)值,其中 x0称为极值点,f(x0)称为极值,所以极值点是实数而不是点.(2)函数在闭区间上的最值在极值点处或区间端点处取得.技法三 基本初等函数 1.指数的概念及运算性质:(1)(n√a)n=a(n∈N*);当 n 为奇数时,n√an=a;当 n 为偶数时,n√an=|a|;(2)正数的分数指数幂的意义:amn=n√am;a- mn = 1amn= 1n√am(a>0,m、n∈N*,且 n>1).2.对数...