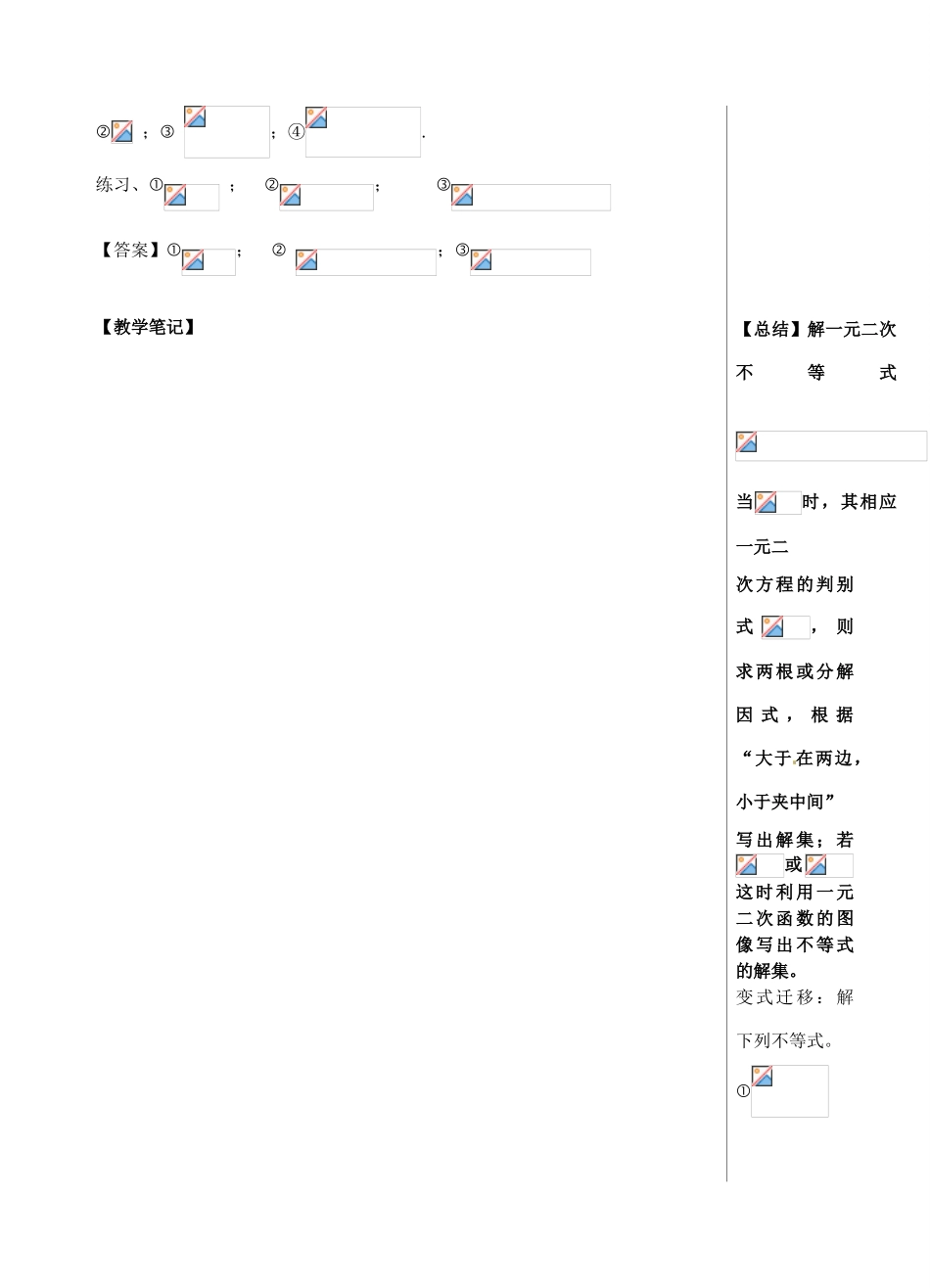
江西省宜春中学高中数学 2.4.2 二次函数导学案 新人教版必修 1【教学目标】 1.理解二次函数、一元二次方程及一元二次不等式的关系; 2.能通过二次函数的图像写出一元二次不等式的解集; 3.了解数形结合思想在解题中的应用。【教学过程】一、预习导航,要点指津 1、回顾二次函数的图像和性质 (1)二次函数的开口方向、顶点坐标、与 轴 的交点坐标 及对称轴分别是什么?并作出它的草图. 开口方向:向上; 顶点坐标:; 与轴的交点坐标:; ④ 对称轴为: ⑤ 单调增区间为,单调减区间为。(2)、根据草图填空:当 或 3 时,,即;当时,函数的图像位于轴的下方,则,即(填或).故不等式的解集是;当,函数的图像位于轴的上方,则,即(填或).故不等式的解集是总结归纳:上述方法可以推广到求一般的一元二次不等式或 的 解 集 。 利用 二 次 函 数的 图 像 解 一元 二 次 不 等式的步骤是:先求对应方程的根,再画 出 不 等 式所 对 应 的 二次 函 数 的 图像 , 并 标 出图 像 与轴交点 【教学笔记】-5-4-3-2-165432y-61-5 -4 -3 -2 -165432xO1-6的横坐标,曲线在轴上方部分的点的横坐标的集合,就是不等式大于零的解集;曲线在轴下方部分的点的横坐标的集合,就不是不等式小于零的解集。2、三个二次的关系完成以下表格。二次函数()的图象一元二次方程有两相异实根有两相等实根无实根的根二、自 主 探 索独立 思 考(约10 分钟) 例 1 、 解 下 列不等式: ④ 【答案】; ; ;④.练习、 ; ; 【答案】; ;【教学笔记】【总结】解一元二次不等式当时,其相应一元二次方程的判别式, 则求两根或分解因 式 , 根 据“大于 在两边,小于夹中间”写出解集;若或这时利用一元二次函数的图像写出不等式的解集。变式迁移:解下列不等式。 【答案】 例 2、解下列关于的不等式(1) (2)【答案】(1)不等式的解集为:当时,;当时,;当时,.(2)不等式的解集为:当时,;当时,;当时,;当时,;当时,【总结】当不等式中含有参数时,必须分类讨论。分类是由不确定和不统一而引起的,分类标准是根据需 要而设定的,“需要”可能是:是什么不等式(一元一次?一元二次?);开口方向如何;根的判别式的正、负;根的大小等。 例 3、已知二次函数的二次项系数为,且不等式的解集为(1, 3)...