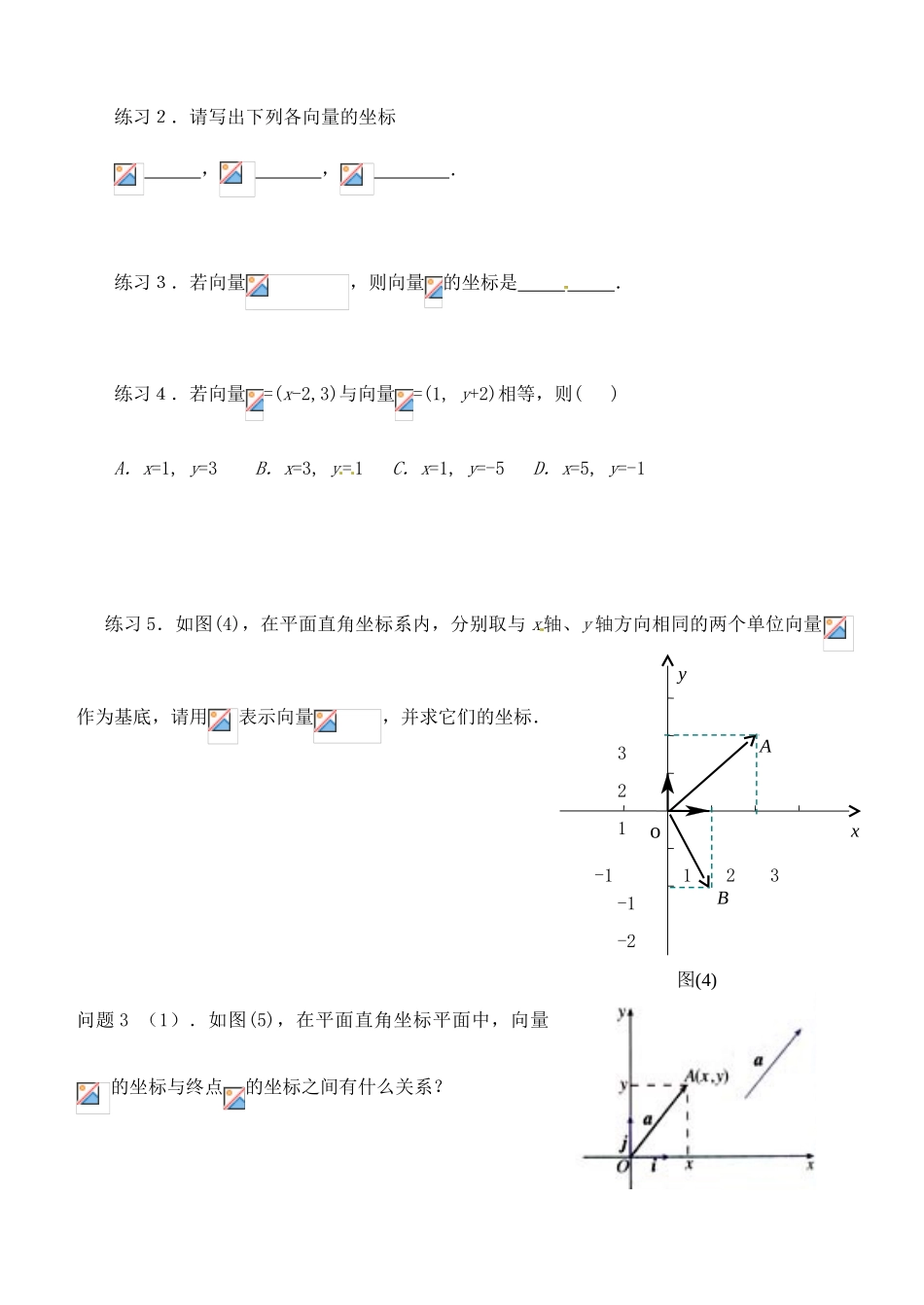
O河南省淇县 2011-2012 学年高一数学下学期 2.3.2《平面向量的正交分解及坐标表示》导学案 沪教版一、教学任务分析(1)、通过力的分解问题,感受平面向量的正交分解与现实的紧密联系; 掌握平面向量的正交分解.(2)、类比平面直角坐标系中,点用有序实数对表示,掌握平面向量的坐标表示.二、教学重点、难点重点:平面向量的正交分解及坐标表示.难点:平面向量的正交分解及坐标表示.三、教学过程 (一)、温故知新 平面向量基本定理:如果、是同一平面 内的两个不共线向量,那么对于这一平面内的任意向量, ,使 .我们把不共线的向量、叫做表示这一平面内所有向量的一组 .(二)创设情境 问题 1 如图(1),光滑斜面上一个木块受到重 力的作用,会产生哪两个效果?一是 ;一是 . 图(1)问题 2 由平面向量基本定理,对于平面内的任意向量,均可以分解为不共线的两个向量吗?(三)、讲授新课1.平面向量的正交分解把一个向量 ,叫做把向量正交分解.练习 1.如图(2),请把导弹刚发射后某时刻的速度正交分解.图(2)思考:我们知道,在平面直角坐标系中,每一个点都可用一对有序实数(即它的坐标)表示.对直角坐标平面内的每一个向量,如何表示呢?2.平面向量的坐标表示 如图(3),在平面直角坐标系中,分别取与轴、轴方向相同的两个单位向量 、作为基底.对于平面内的一个向量,由平面向量基本定理可 知 , ,使得 . ①这样,平面内的任一向量都可由 x、y 唯一确定,我们把有序数对叫做向量的坐标,记作 ② 图(3)其中 叫做在轴上的坐标, 叫做在轴上的坐标,②式叫做向量的坐标表示.巩固提高: 练习2.请写出下列各向量的坐标 , , .练习3.若向量,则向量的坐标是 .练习4.若向量=(x-2,3)与向量=(1, y+2)相等,则( )A.x=1, y=3 B.x=3, y=1 C.x=1, y=-5 D.x=5, y=-1练习 5.如图(4),在平面直角坐标系内,分别取与 x轴、y 轴方向相同的两个单位向量作为基底,请用表示向量,并求它们的坐标.问题 3 (1).如图(5),在平面直角坐标平面中,向量的坐标与终点的坐标之间有什么关系?图(4) 1 2 3 -1 -1 -2 1 2 3xoABy(2).如图(6),若向量的起点不在原点,怎样得到的坐标? 因此,在平面直角坐标系内,每一个平面向量都可以用一有序实数对唯一表示.(四)、典例剖析 如图(7),分别用基底 、表示向量,并求它们的坐标.变式练习: xODCBAy图(5)图(6)图(7)...