浙江省瓯海区三溪中学高一数学 函数的奇偶性教学案

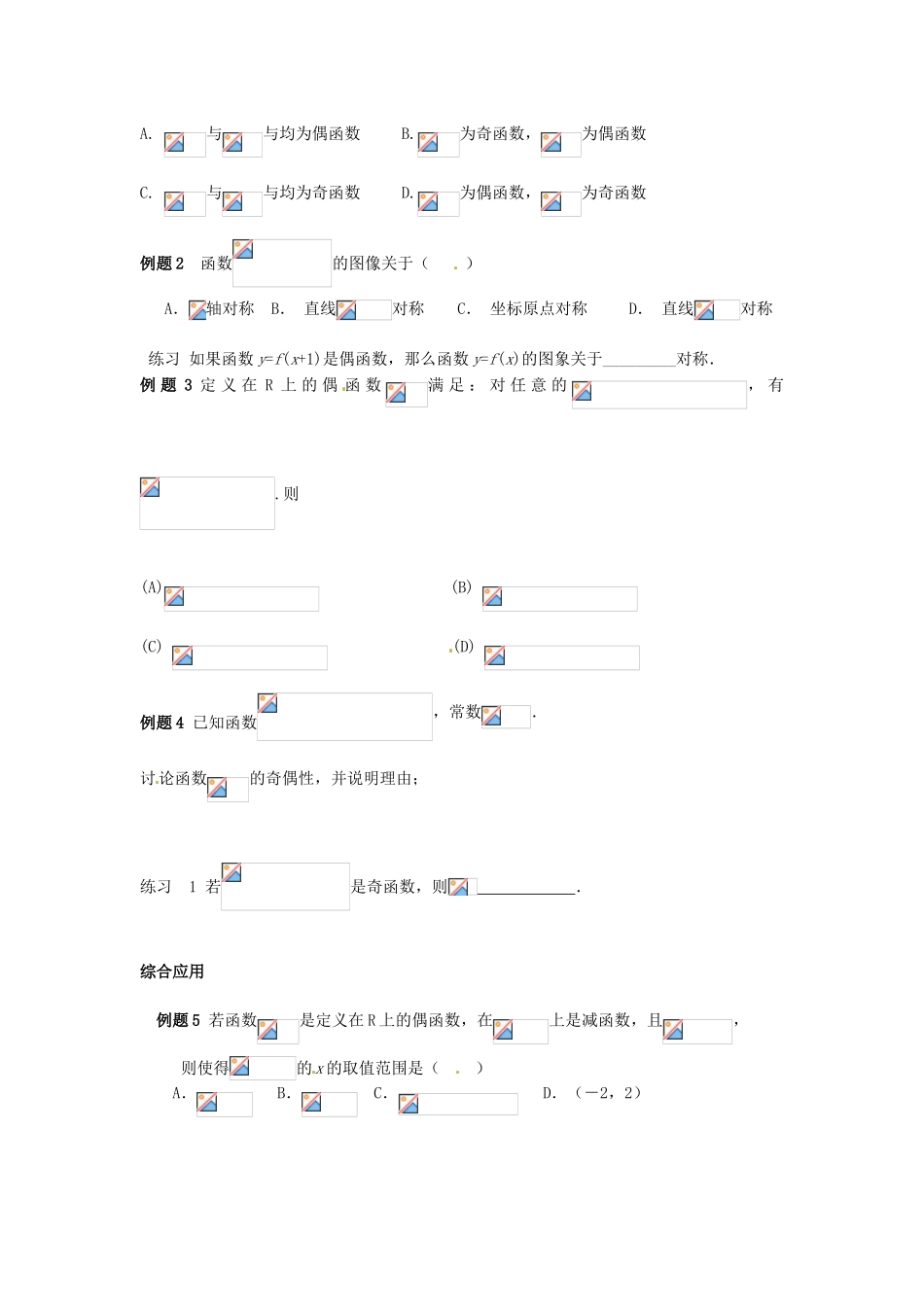
浙江省瓯海区三溪中学高一数学教学教学案：函数的奇偶性学校_________ 班级_________ 姓名_________基础回顾 一、下图左为偶函数下图右为奇函数 二、下列函数中在定义域上为偶函数的有_________，为奇函数的有________，不具有奇偶性的是________ 1、 2、 3、 4、三、 函数的奇偶性：如果对于函数 f(x)的定义域内任意一个 x 都有______________________,那么函数 f(x)就叫做奇函数，奇函数的图像关于_______对称；如果对于函数 y=f(x)的定义域内任意一个 x 都有___________,那么函数 f(x)就叫做偶函数，偶函数的图像关于_______ 对 称 。 当 函 数 f(x) 是 奇 函 数 或 偶 函 数 时 ， 称 函 数 具 有 _______ 性 。 结论：（1）若函数 f(x)具有奇偶性，则其定义域必定关于________对称； （2）若 f(x)是奇函数，且 f(0)有意义，则必定有 f(0)=________。例题1 函数 的 奇 偶 性为________练习 1 若函数是偶函数，则实数的值为 (A) (B) (C) (D)练习 2 若函数与的定义域均为 R，则A. 与与均为偶函数 B.为奇函数，为偶函数C. 与与均为奇函数 D.为偶函数，为奇函数例题 2 函数的图像关于（ ） A．轴对称 B． 直线对称 C． 坐标原点对称 D． 直线对称练习 如果函数 y=f(x+1)是偶函数，那么函数 y=f(x)的图象关于_________对称．例 题 3 定 义 在 R 上 的 偶 函 数满 足 ： 对 任 意 的， 有.则(A) (B) (C) (D) 例题 4 已知函数，常数． 讨论函数的奇偶性，并说明理由；练习 1 若是奇函数，则 ．综合应用 例题 5 若函数是定义在 R 上的偶函数，在上是减函数，且，则使得的x 的取值范围是（ ）A． B． C． D．（－2，2）练习 已知函数是定义在上的偶函数. 当时，，则 当时， 提升 直线与曲线有四个交点，则的取值范围是 . 本节课主要学习了函数的奇偶性的概念以及判断函数在定义域上的奇偶性的方法。 1 函数具有奇偶性必须满足（1）定义域在数轴上关于原点对称 （2）f(-x)=f(x)或 f(-x)=-f(x)在定义域内恒成立 若函数定义域关于原点不对称，则函数为非奇非偶函数。2 奇函数、偶函数的图像特征 奇函数的图像关于原点成中心对称图形 偶函数的图像关于 y 轴成轴对称图形