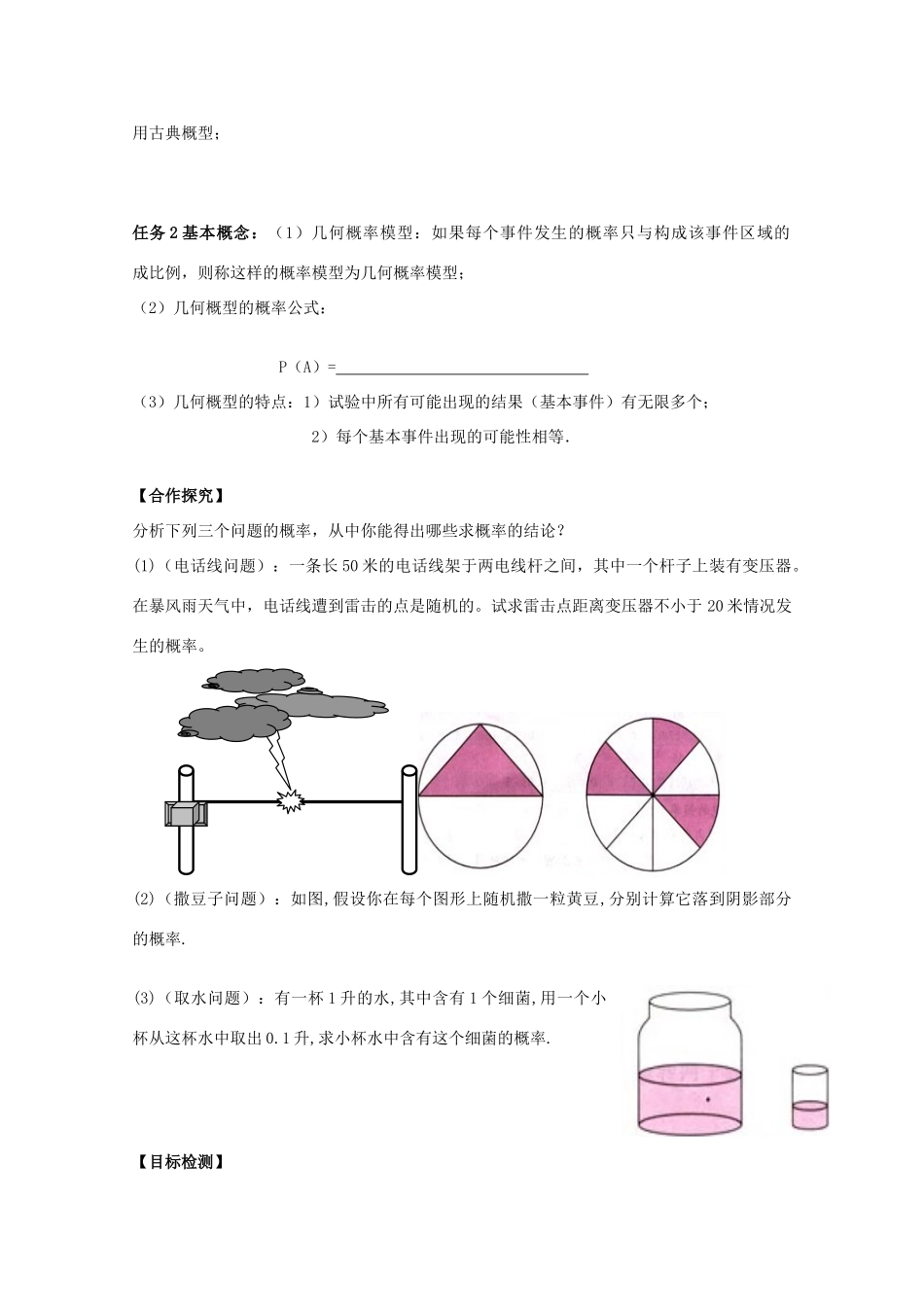
湖南省邵阳市隆回二中高一数学导学案:第三章 概率 3.3.1 几何概型 (新人教 A 版必修 3)【学习目标】(1)知识与技能:① 通过师生共同探究,体会数学知识的形成,正确理解几何概型的定义、特点,掌握几何概型的概率公式:② 会根据古典概型与几何概型的区别与联系来判断某种概型是古典概型还是几何概型;会进行简单的几何概型的概率计算,培养学生从有限向无限探究的意识。(2)情感态度与价值观:培养学生积极思考,理论联系实际,严谨勤学的学习习惯。【自主学习】任务 1:阅读教材 P135—136,独立完成下列问题 问题 1:(回顾) 古典概型的特点及其概率公式:练习1.(赌博游戏):甲乙两赌徒掷色子,规定掷一次谁掷出 6 点朝上则谁胜,请问甲、乙赌徒获胜的概率谁大? 2.(转盘游戏):图中有两个转盘.甲乙两人玩转盘游戏,规定当指针指向 B 区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少?① ②分析:指针指向的每个方向都是等可能性的,但指针所指的位置却是无限个的,因而无法利BNBN BNNBBNB用古典概型;任务 2 基本概念:(1)几何概率模型:如果每个事件发生的概率只与构成该事件区域的 成比例,则称这样的概率模型为几何概率模型;(2)几何概型的概率公式:P(A)= (3)几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.【合作探究】分析下列三个问题的概率,从中你能得出哪些求概率的结论? (1)(电话线问题):一条长 50 米的电话线架于两电线杆之间,其中一个杆子上装有变压器。在暴风雨天气中,电话线遭到雷击的点是随机的。试求雷击点距离变压器不小于 20 米情况发生的概率。 (2)(撒豆子问题):如图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到阴影部分的概率.(3)(取水问题):有一杯 1 升的水,其中含有 1 个细菌,用一个小杯从这杯水中取出 0.1 升,求小杯水中含有这个细菌的概率.【目标检测】1.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于 10 分钟的概率.2 在 500的水中有一个草履虫,现在从中随机取出 2水样放到显微镜下观察,则发现草履虫的概率为( )A.0.5 B.0.4 C.0.004 D.不能确定学习反思:本节课我学到了什么?本节课我的学习效率如何?本节课还有哪些没学懂?