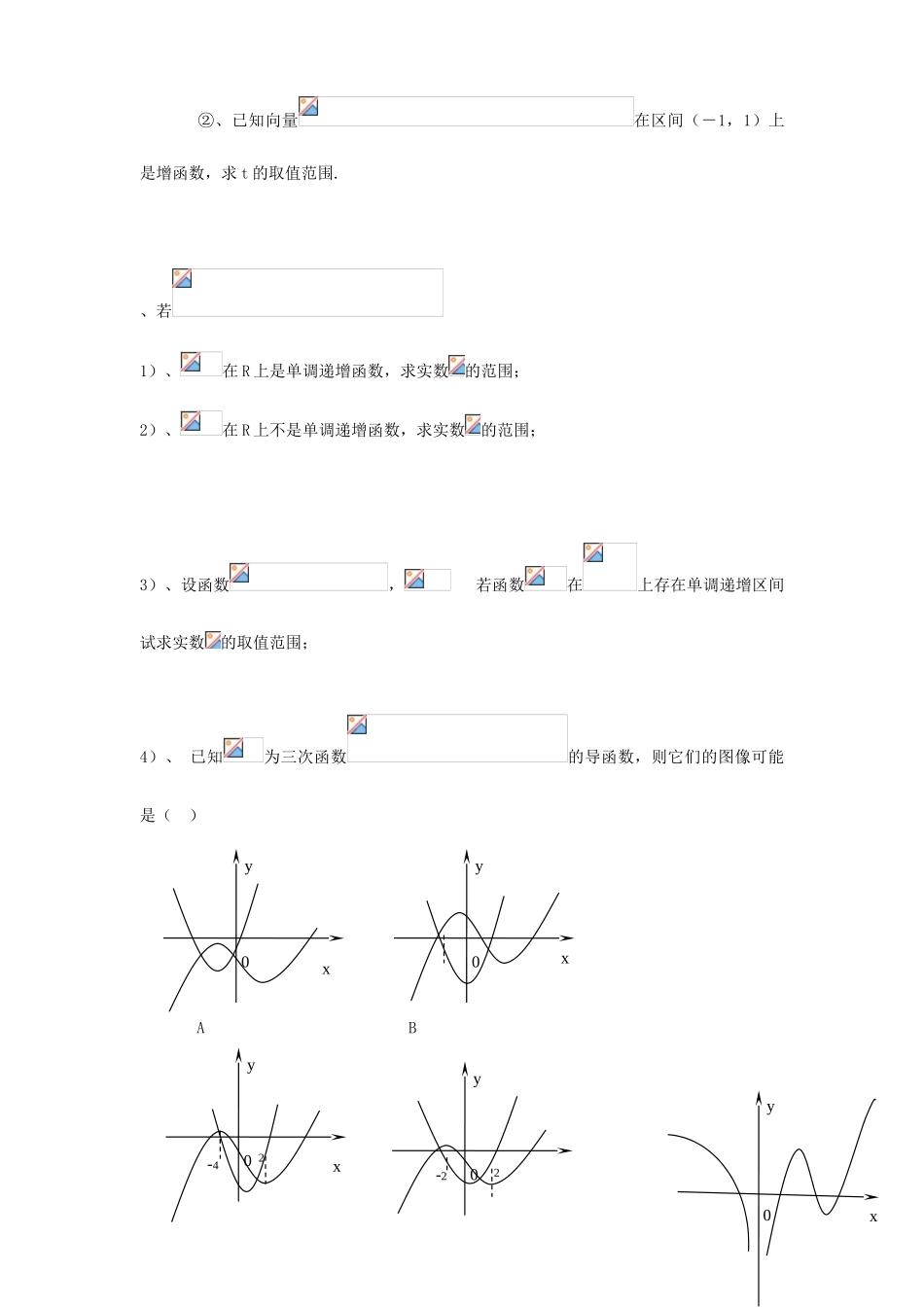
重庆市开县中学高中数学 导数在研究函数中的应用导案 新人教版A 版选修 1-1课程标准学习目标1、结合实例,借助几何直观探索并初步体会函数的单调性与导数的关系。2、能利用导数研究函数的单调性,并会求不超过三次的多项式函数的单调区间,并能将函数与其导数图象进行比较。3、结合函数的图象,能说出函数在某点取得极的必要条件和充分条件。4、会用导数求不超过三次的多项式函数的极大值、极小值,并能画出它们的简图。5、会求在给定区间上不超过三次的多项式函数的最大值、最小值。重难点重点:利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间。难点:函数在某点取得极值的必要和不充分条件。学习过程评价任务(内容、问题、试题)学习活动(方式、行为、策略)[模块一] 函数的单调性与导数问题 1、学习 P22 观察图 1.3-1,说出运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态与的正负关系。问题 2、看书 P23 指出函数的单调性与其导函数正负的关系。(1)填空:在某个区间(a, b)内,如果 ,那么函数在这个区间内单调递增;如果 ,那么函数在这个区间内单调递减。(2)连续可导函数在区间(a, b)单调递增(或递减)时,满足怎样的条件?是函数在区间(a, b)上单调递增的 条件。问题 3、求函数单调区间的步骤: 例题 1、已知函数的图象过点 P(0,2),且在点 M(-1,f(-1))处的切线方程为. (Ⅰ)求函数的解析式; (Ⅱ)求函数的单调区间.例题 2、(1)、讨论函数的单调性(2)、讨论函数的单调性例题 3、、确定函数 求 单调增区间单调减区间 ②、已知向量在区间(-1,1)上是增函数,求 t 的取值范围.、若1)、在 R 上是单调递增函数,求实数的范围;2)、在 R 上不是单调递增函数,求实数的范围;3)、设函数, 若函数在上存在单调递增区间试求实数的取值范围; 4)、 已知为三次函数的导函数,则它们的图像可能是( ) A B20y-4x0yx0yx0y-22x0y C D 、设函数的图像如图,则导函数的图像可能为( ) A B C D 、设函数的导函数的图像如图,则导函数的图像可能为( ) A C D 变式:求下列函数的单调区间:x0yx0yx0yx0y0y20yx12x0y120yx120y1 2(1);(2)拓展训练:1、已知函数的单调增区间为(-2,3),求 a、b 的值。2、若,则的大小关系 。 3、已知定义在正实数集上的函数,其中,设两曲线,有公共点且在该点处的切线相同 (1)...