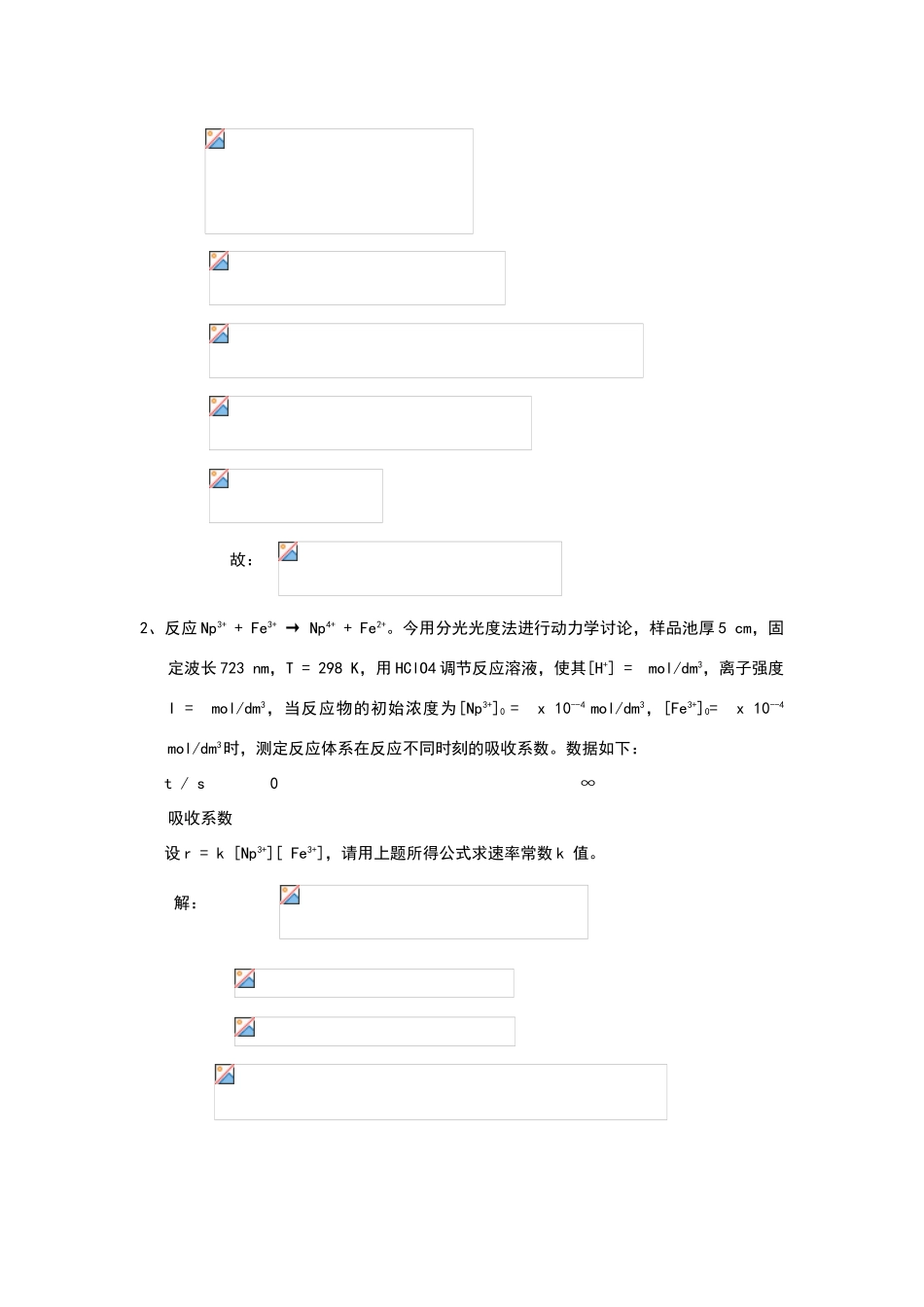
《化学反应动力学》第 三、四章习题1、试推导 A + B → P ,当其为二级反应 r = k[A][B]时,其积分速率方程为: ln{1 + Δ0(P0 - P∞)/ [A]0(Pt – P∞)} = ln [B]0 / [A]0 +Δ0k t 式中,P 为用物理仪器测定的体系的某种物理性质(如吸光系数),该性质与浓度有线性关系,Δ0 = [B]0 - [A]0 解: 设 B 过量 A + B → P t = 0 [A]0 [B]0 P0 = [A]0λA+ [B]0λB + λM (1) t = t [A]0-x [B]0-x Pt = ([A]0-x) λA+ ([B]0-x) λB + λM (2) t = ∞ [B] 0 - [A]0 P∞ = ([B]0- [A]0) λB + λM (3) 据二级反应速率方程: (1)-(3)得:P0 – P∞= [A]0(λA+λB) , 即: (1)-(2)得:P0 – Pt=λAx + λB x 由上面两式可得: 故: 2、反应 Np3+ + Fe3+ → Np4+ + Fe2+。今用分光光度法进行动力学讨论,样品池厚 5 cm,固定波长 723 nm,T = 298 K,用 HClO4 调节反应溶液,使其[H+] = mol/dm3,离子强度I = mol/dm3,当反应物的初始浓度为[Np3+]0 = x 10--4 mol/dm3,[Fe3+]0= x 10--4 mol/dm3时,测定反应体系在反应不同时刻的吸收系数。数据如下: t / s 0 ∞吸收系数 设 r = k [Np3+][ Fe3+],请用上题所得公式求速率常数 k 值。解: t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 t= k= ×103 dm3mol-1s-1 考虑活度: 3、推导对峙反应 的弛豫过程动力学方程为:。要求写出详细的推导过程,指出满足上式的条件。式中 为弛豫变量。 解: 速率方程: (1) 设各组元与平衡值有一偏离, 则 将以上三式代入(1)式: 忽略项,得: 故: 4、用超声法讨论异构化反应,测定化合物转动异构化反应的弛豫时间为 10-6秒,假如平衡时占优势的异构体的比例为 80%,试测定占优势异构化反应的速率常数。 解:设两种异构体分别为 A 和 B,其中 B 占优势 则: 对 1-1 级反应,驰豫时间 ,即 联立方程 , ,可解得: 占优势的异构化反应速率常数 5、What is the temperature dependence of a slow solution reaction What is the temperature dependence of the rate constant for...