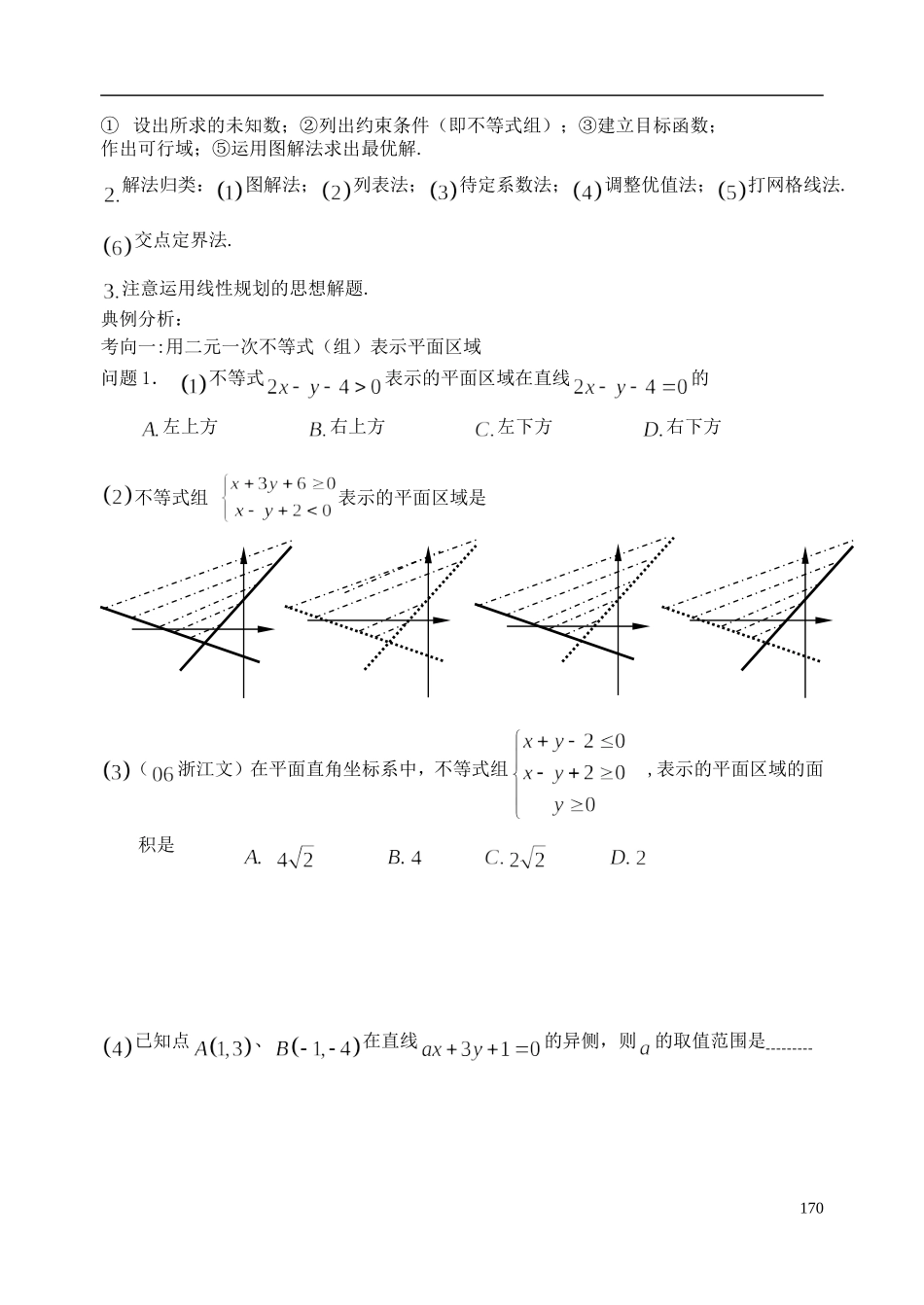
课题:二元一次不等式(组)与简单的线性规划问题考纲要求:① 会从实际情境中抽象出二元一次不等式组.② 了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.③ 会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.教材复习二元一次不等式表示平面区域.一般地,二元一次不等式在平面直角坐标系中表示直线某一侧的所有点组成的平面区域(半平面)不含边界线;不等式所表示的平面区域(半平面)包括边界线.判定不等式(或)所表示的平面区域时,只要在直线的一侧任意取一点,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域。由几个不等式组成的不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.另外:规律总结:,(视“”为“”,“”为“”),分别计算: 的符号与“”或“”的积; 的符号与“”或“”的积; “左下负,右上正”.线性规划问题的图解法: 名 称意 义线性约束条件由的一次不等式(或方程)组成的不等式组,是对的约束条件目标函数关于的解析式线性目标函数关于的一次解析式可行解满足线性约束条件的解叫做可行解可行域所有可行解组成的集合叫做可行域最优解使目标函数达到最大值或最小值的可行解线性规划问题求线性目标函数在线性约束条件下的最大值或最小值的问题基本知识方法:用图解法解决线性规划问题的一般步骤169① 设出所求的未知数;②列出约束条件(即不等式组);③建立目标函数;作出可行域;⑤运用图解法求出最优解.解法归类:图解法;列表法;待定系数法;调整优值法;打网格线法.交点定界法.注意运用线性规划的思想解题.典例分析:考向一:用二元一次不等式(组)表示平面区域问题 1. 不等式表示的平面区域在直线的左上方 右上方左下方 右下方不等式组 表示的平面区域是(浙江文)在平面直角坐标系中,不等式组 ,表示的平面区域的面积是 已知点、在直线的异侧,则的取值范围是 170考向二:求目标函数的最值问题 2.(海南文)设满足则有最小值,最大值 有最小值,无最大值有最大值,无最小值 既无最小值,也无最大值 (陕西文)设满足约束条件,目标函数的最小值是 ,最大值是 (辽宁)已知变量满足约束条件则的取值范围是 171(湖南)已知则的最小值是 考向三: 求参数的取值或范围问题 3.(全国新课标Ⅱ)已知0a , ,x y 满足约束条件13(...