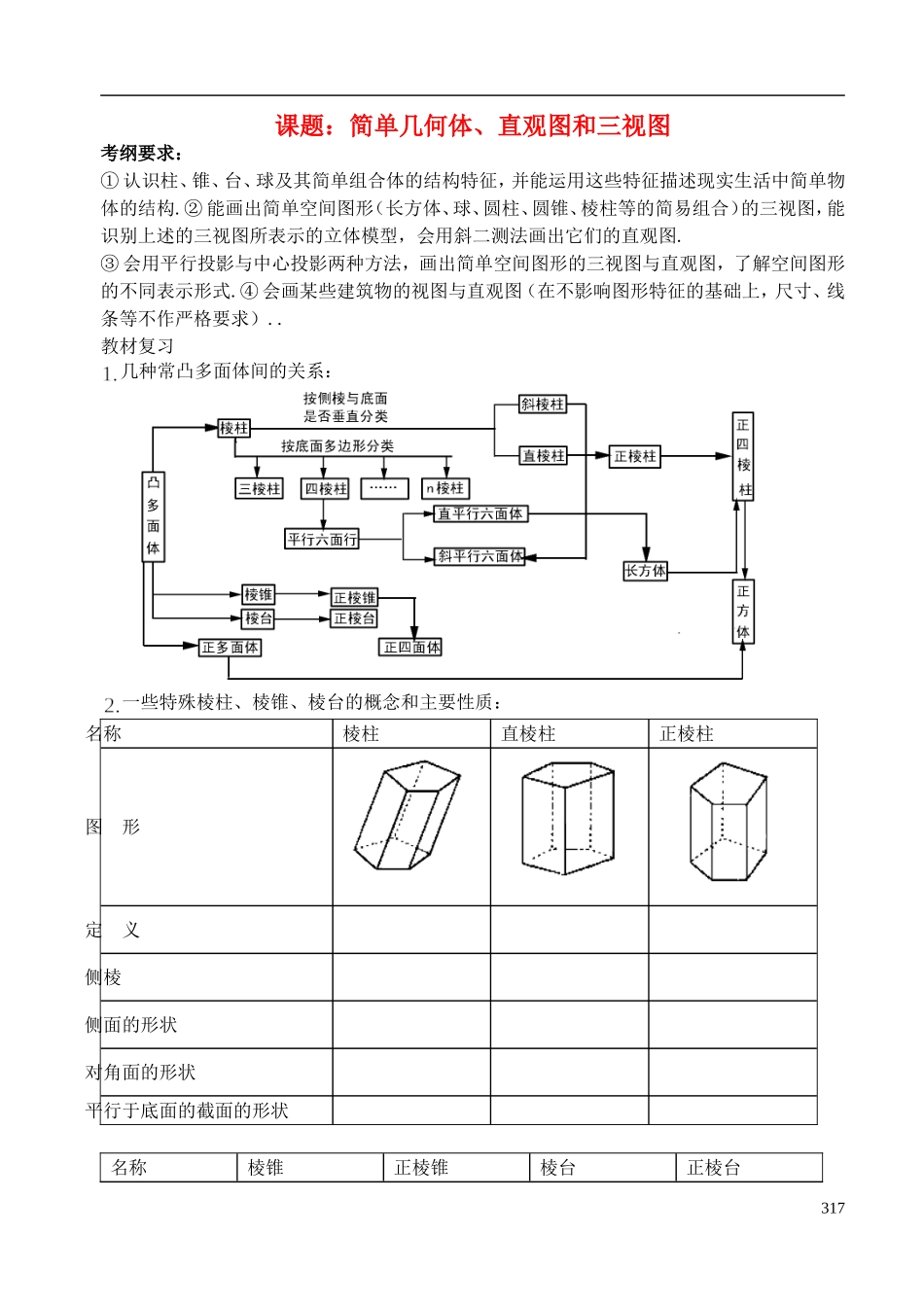
课题:简单几何体、直观图和三视图考纲要求:① 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.② 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测法画出它们的直观图.③ 会用平行投影与中心投影两种方法,画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.④ 会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求)..教材复习几种常凸多面体间的关系:一些特殊棱柱、棱锥、棱台的概念和主要性质:名称棱柱直棱柱正棱柱图 形定 义侧棱侧面的形状对角面的形状平行于底面的截面的形状名称棱锥正棱锥棱台正棱台 317图形定义侧棱侧面的形状对角面的形状平行于底的截面形状其他性质几种特殊四棱柱的特殊性质名称特殊性质平行六面体直平行六面体长方体正方体简单旋转体几何体旋转图形旋转轴圆柱圆锥圆台球基础知识方法三视图画法的关键是要分清观察者的方向,应从前面到后面,左面到右面,上面向下面三个方向去观察图形;画三视图时要做到“长对正,宽相等,高平齐”。 斜二测画法要注意其规则: “横不变,纵折半,保平行”.典例分析:考点一 空间几何体的结构特征 318问题 1.(哈师大附中月考)下列结论正确的是各个面都是三角形的几何体是三棱锥以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥圆锥的顶点与底面圆周上的任意一点的连线都是母线有下列四个命题:① 底面是矩形的平行六面体是长方体;② 棱长相等的直四棱柱是正方体;③ 有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④ 对角线相等的平行六面体是直平行六面体.其中真命题的个数是 (江西文)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下个命题中,假命题是等腰四棱锥的腰与底面所成的角都相等等腰四棱锥的侧面与底面所成的二面角都相等或互补等腰四棱锥的底面四边形必存在外接圆等腰四棱锥的各顶点必在同一球面上(全国Ⅱ文)下面是关于三棱锥的四个命题:① 底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.② 底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.③ 底面是等边三角形,侧面的面积都相等的三棱锥是正三棱...