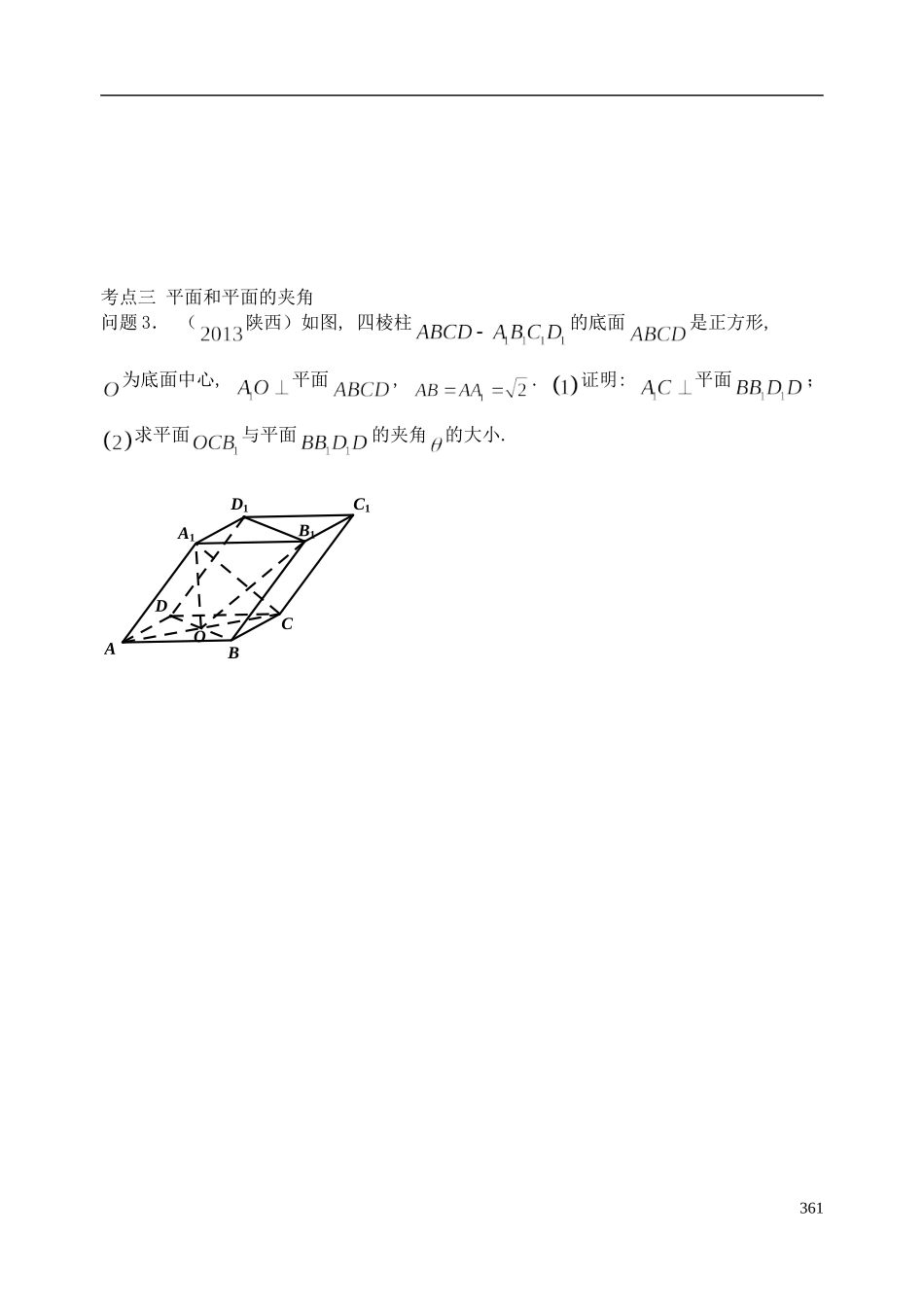
课题:空间向量与立体几何考纲要求:① 理解直线的方向向量和平面的法向量.② 能向量语言表述直线与直线、直线与平面、平面与平面的垂直关系、平行关系;③能用向量方法证明有关直线和平面位置关系的一些定理;④能用向量方法解决直线与直线、直线与平面、平面与平面的夹角计算问题,了解向量方法在研究立体几何问题中的作用.教材复习异面直线所成角:设、分别为异面直线、的方向向量,则与的夹角直线、所成的角 范围 求法 直线与平面所成的角:①直线与平面所成角的范围是 ;② 设是斜线 的方向向量,是平面的一个法向量,设斜线与平面所成的角为,则 两平面的夹角:设和分别是平面和的一个法向量,平面和的夹角为,则 空间任意两点、间的距离即线段的长度:设、,则 .点到平面距离:如右图,斜线交平面于点,359a1n�2n�1n�2n�a平面一个法向量为,斜线的一个方向向量为,则点到平面的距离为 直线 的方向向量是,平面的法向量为,则 ∥ . 直线 的方向向量是,平面的法向量为,则 . 平面的法向量为,平面的法向量为,则 . 平面的法向量为,平面的法向量为,则∥ . 典例分析:考点一 异面直线所成的角问题 1. (陕西)如图,在空间直角坐标系中有直三棱柱111ABCA B C,12CACCCB,则直线1BC 与直线1AB 夹角的余弦值为55 53 2 55 35考点二 直线和平面所成的角问题 2.(山东)已知三棱柱的侧棱与底面垂直,体积为,底面是边长为的正三角形.若为底面的中心,则与平面所成角的大小为 360考点三 平面和平面的夹角问题 3. (陕西)如图, 四棱柱的底面是正方形, 为底面中心, 平面, . 证明: 平面;求平面与平面的夹角的大小. 361OD1B1C1DACBA1考点四 求点到平面的距离问题 4.(江西)如图,在长方体中,,,点在棱上移动.略;当为的中点时,求点到面的距离;略. (请用多种方法,至少要用向量法)考点五 存在性问题问题 5:(北京)如图,在三棱柱中,是边长为的正方形,平面平面,,.求证:平面(这里不做);求二面角的余弦值(这里不做);证明:在线段存在点,使得,并求的值.362课后作业: (洛阳联考)在平面直角坐标系中,点的坐标为,点的坐标为,将直角坐标平面沿轴折成直二面角,则两点间的距离为 (辽宁六校联考)如图,平面平面,为正三角形,四边形为矩形,为的中点,与平面所成的角为.当长度为时,求点到平面的距离;二面角的大小是否与长度有关?请说明理由.363走向...