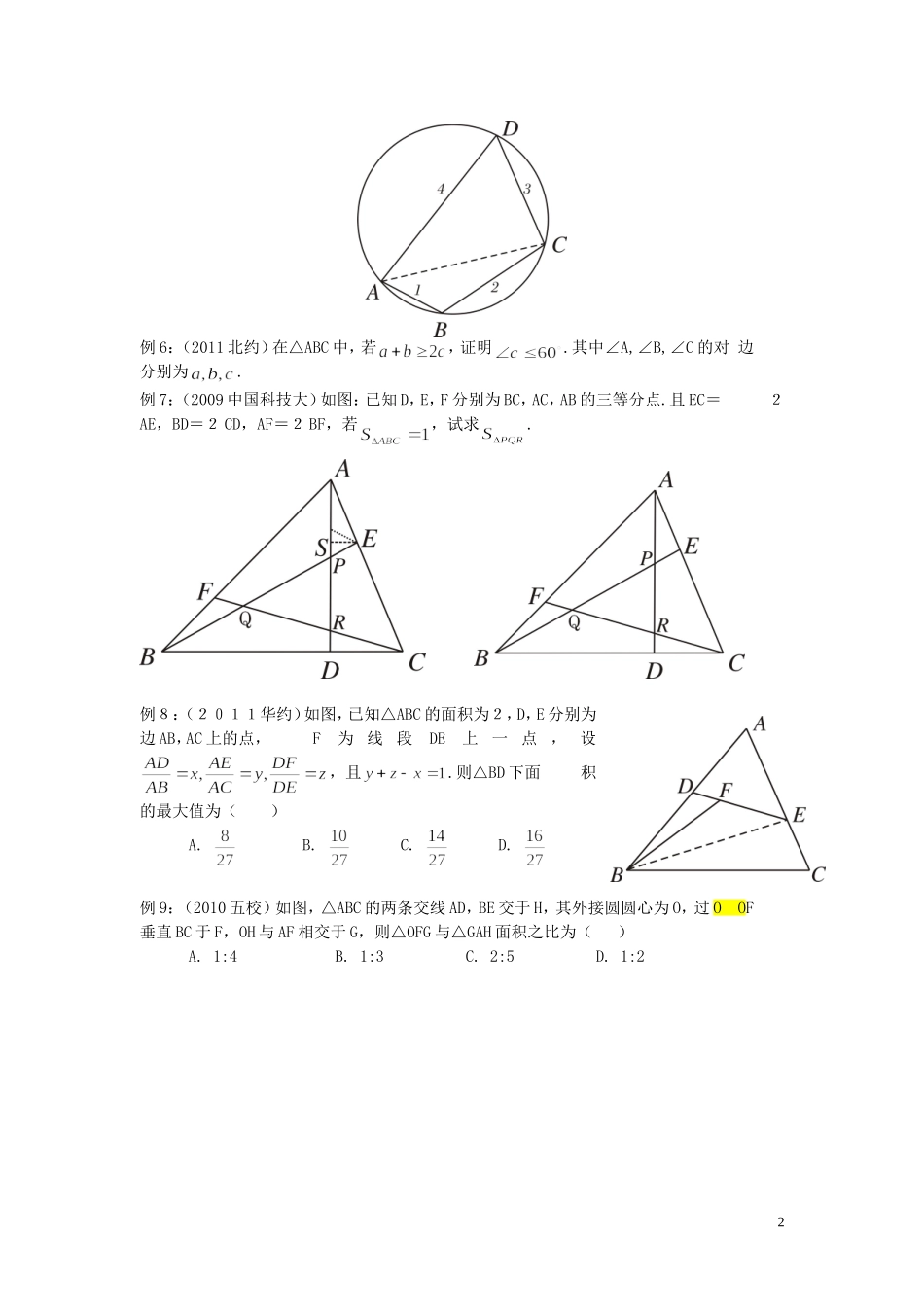
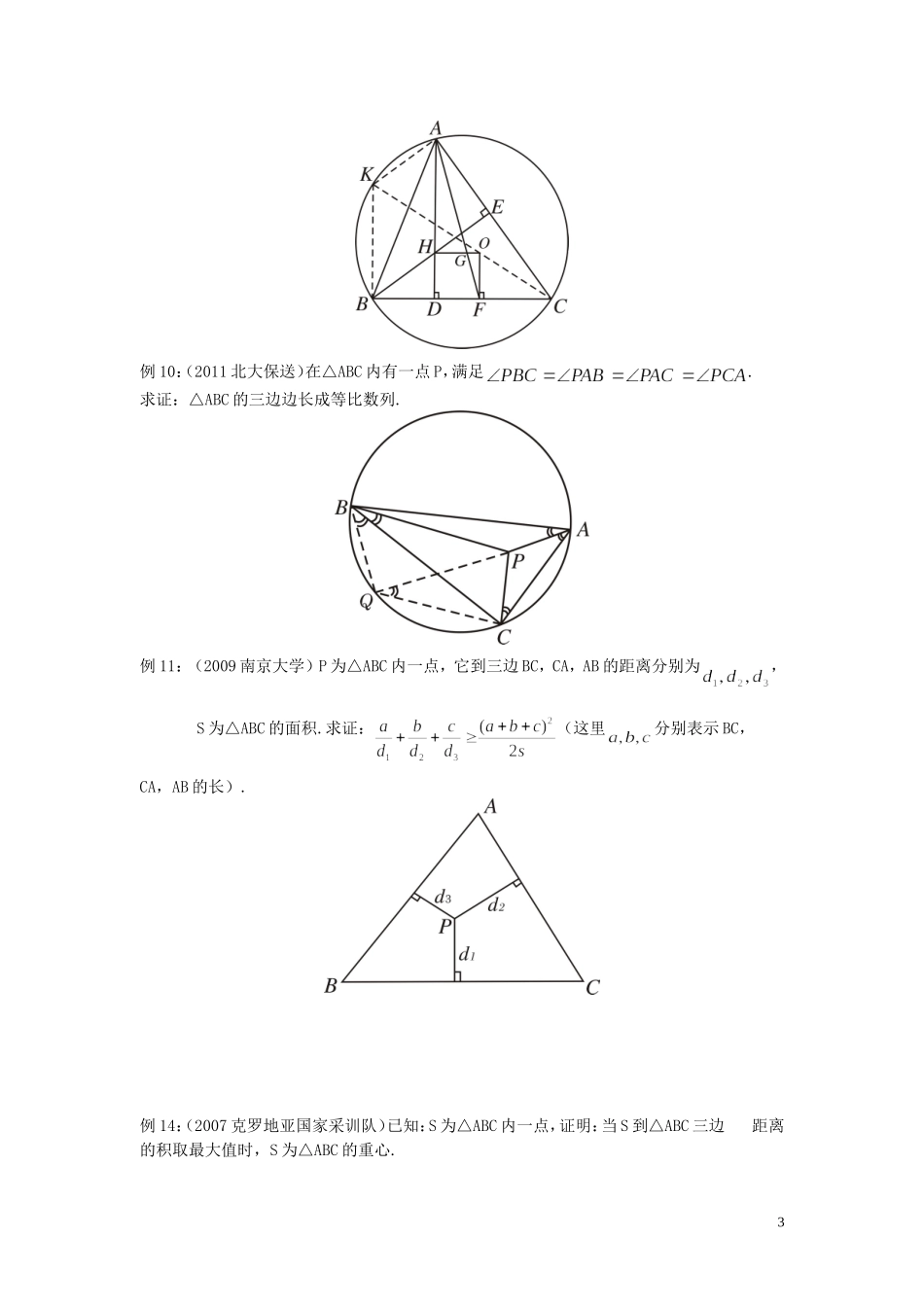
平面几何一、考试要求:平面几何是自主招生考试中北约、华约、卓越共同考查的内容,主要考查平面图形中三边角关系以及长度、角度、面积的计算;考查学生逻辑思维能力,推理认证 能 力 及计算能力.二、知识准备:定理:梅涅劳斯定理:设△ABC 的三边 BC、CA、AB 或他们的延长线与一条不经过其 顶点的直线交于 P、Q、R 三点,则. 梅涅劳斯逆定理:设 P、Q、R 分别是△ABC 的三边 BC、CA、AB 或他们的延 长线上三点,若有,则 P、Q、R 三点在同一条直线上.三、题型训练:类型一:凸多边形有关的计算或证明例 1:(2012 北约)求证:若圆内接五边形的两个角都相等,则它为正五边形.例 2:(2008 北约)求证:边长为 1 的正五边形对角线长为.例 4:(2013 北约)如果锐角△ABC 的外接圆圆心为 O,求 O 到三角形三边距离比.例 5:(2009 北大)圆内接四边形 ABCD 中,AB=1,BC=2,CD=3,DA=4.求圆的半径.1例 6:(2011 北约)在△ABC 中,若,证明.其中∠A,∠B,∠C 的对 边 分别为.例 7:(2009 中国科技大)如图:已知 D,E,F 分别为 BC,AC,AB 的三等分点.且 EC= 2AE,BD=2 CD,AF=2 BF,若,试求. 例8:(2011华约)如图,已知△ABC 的面积为2,D,E 分别为边 AB,AC 上的点, F为线段DE上一点,设,且.则△BD 下面 积的最大值为( ) A. B. C. D. 例 9:(2010 五校)如图,△ABC 的两条交线 AD,BE 交于 H,其外接圆圆心为 O,过 O OF 垂直 BC 于 F,OH 与 AF 相交于 G,则△OFG 与△GAH 面积之比为( ) A. 1:4B. 1:3C. 2:5D. 1:22例 10:(2011 北大保送)在△ABC 内有一点 P,满足. 求证:△ABC 的三边边长成等比数列.例 11:(2009 南京大学)P 为△ABC 内一点,它到三边 BC,CA,AB 的距离分别为, S 为△ABC 的面积.求证:(这里分别表示 BC, CA,AB 的长).例 14:(2007 克罗地亚国家采训队)已知:S 为△ABC 内一点,证明:当 S 到△ABC 三边 距离的积取最大值时,S 为△ABC 的重心.3例 15:在锐角△ABC 中,分别为 BC,CA,AB 的中点,O 为△ABC 外接圆的圆 心,若外接圆半径为 1,证明:.4