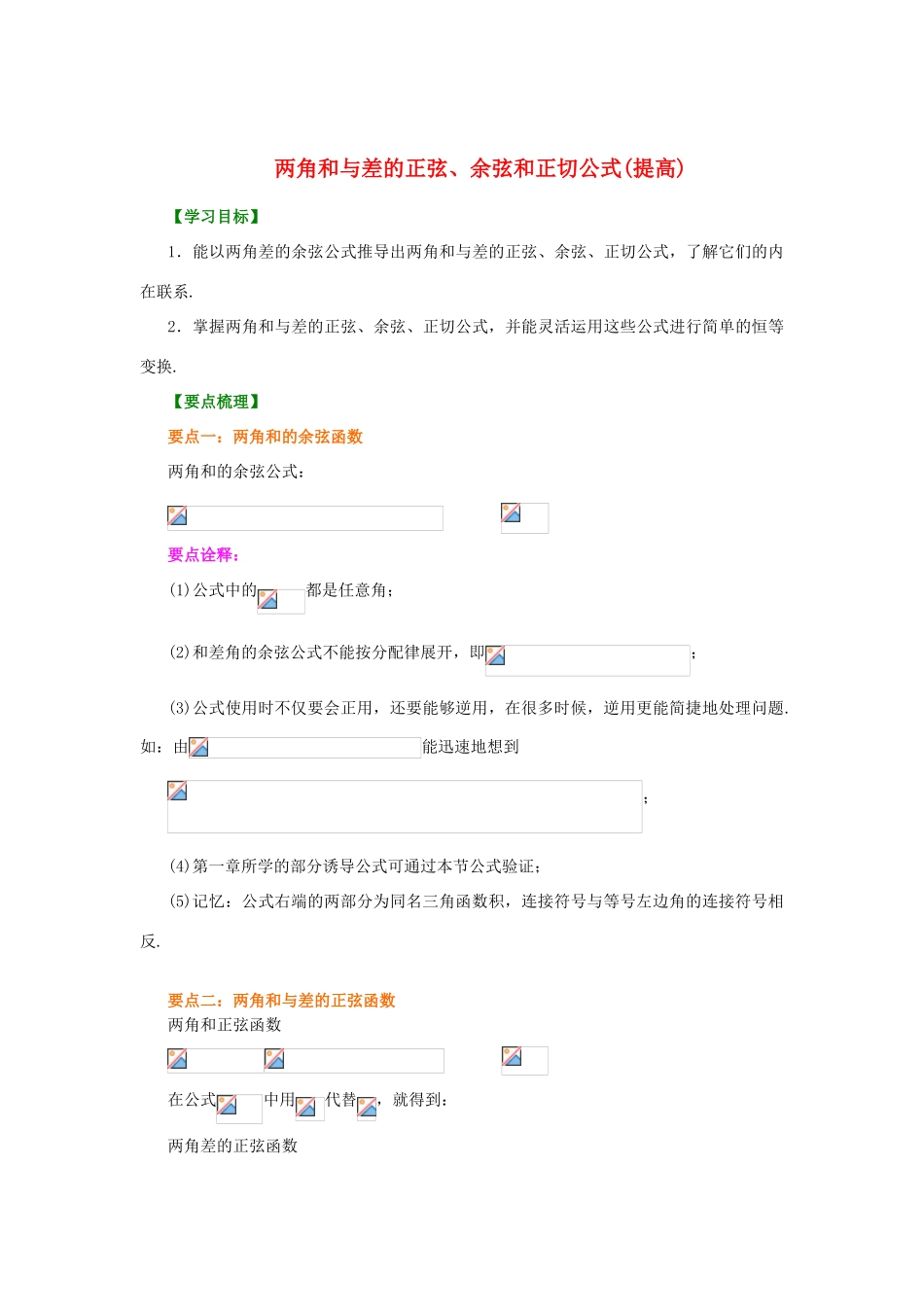
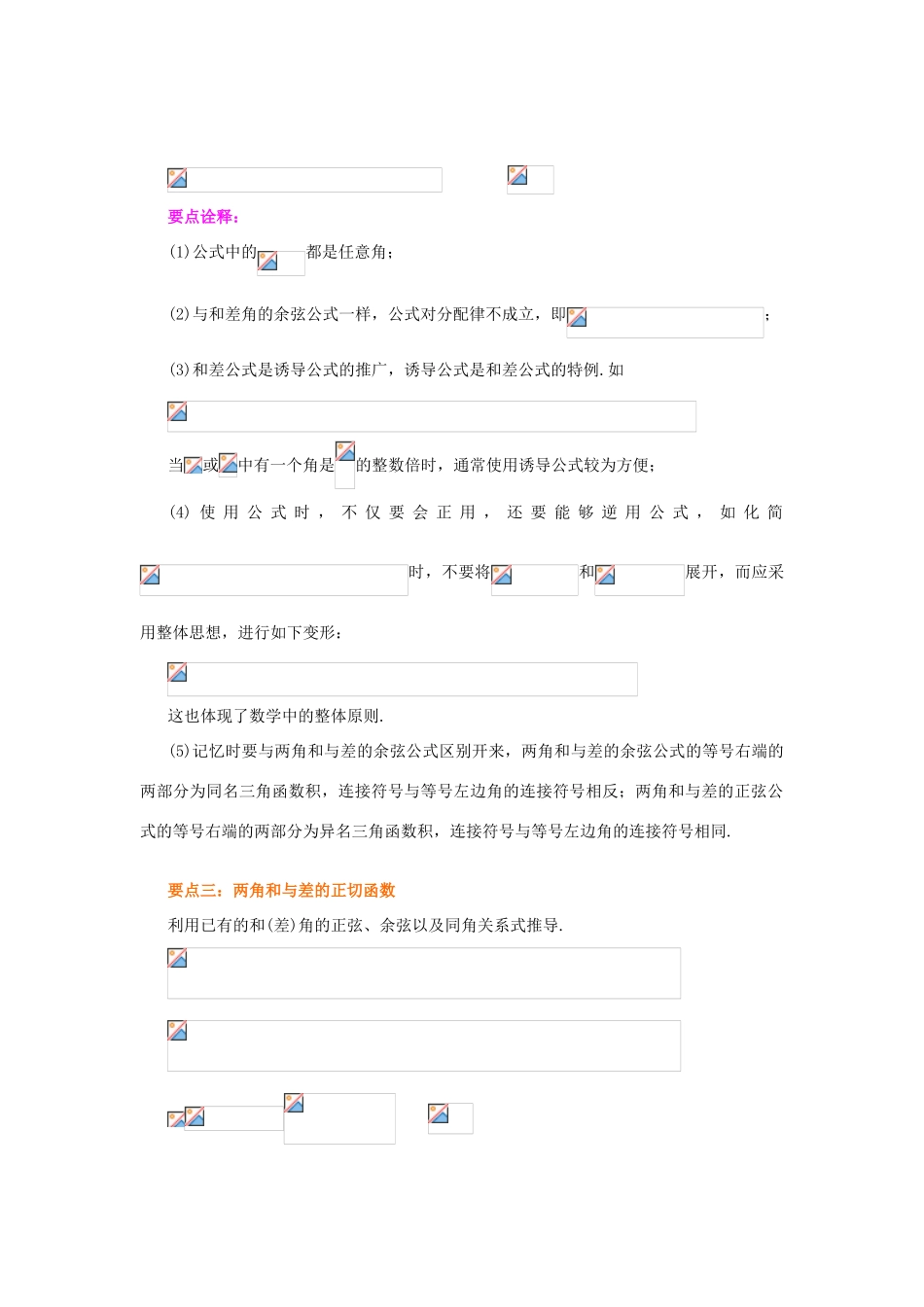
两角和与差的正弦、余弦和正切公式(提高)【学习目标】1.能以两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式,了解它们的内在联系.2.掌握两角和与差的正弦、余弦、正切公式,并能灵活运用这些公式进行简单的恒等变换.【要点梳理】要点一:两角和的余弦函数两角和的余弦公式: 要点诠释:(1)公式中的都是任意角;(2)和差角的余弦公式不能按分配律展开,即;(3)公式使用时不仅要会正用,还要能够逆用,在很多时候,逆用更能简捷地处理问题.如:由能迅速地想到;(4)第一章所学的部分诱导公式可通过本节公式验证;(5)记忆:公式右端的两部分为同名三角函数积,连接符号与等号左边角的连接符号相反.要点二:两角和与差的正弦函数两角和正弦函数 在公式中用代替,就得到:两角差的正弦函数 要点诠释:(1)公式中的都是任意角;(2)与和差角的余弦公式一样,公式对分配律不成立,即;(3)和差公式是诱导公式的推广,诱导公式是和差公式的特例.如当或中有一个角是的整数倍时,通常使用诱导公式较为方便;(4) 使 用 公 式 时 , 不 仅 要 会 正 用 , 还 要 能 够 逆 用 公 式 , 如 化 简时,不要将和展开,而应采用整体思想,进行如下变形:这也体现了数学中的整体原则.(5)记忆时要与两角和与差的余弦公式区别开来,两角和与差的余弦公式的等号右端的两部分为同名三角函数积,连接符号与等号左边角的连接符号相反;两角和与差的正弦公式的等号右端的两部分为异名三角函数积,连接符号与等号左边角的连接符号相同.要点三:两角和与差的正切函数利用已有的和(差)角的正弦、余弦以及同角关系式推导. 要点诠释:(1)公式成立的条件是:;(2)公式的变形: (3)两角和与差的正切公式不仅可以正用,也可以逆用、变形用,逆用和变形用都是化简三角恒等式的重要手段,如就可以解决诸如的求值问题.所以在处理问题时要注意观察式子的特点,巧妙运用公式或其变形,使变换过程简单明了.(4)公式对分配律不成立,即.要点四:理解并运用和角公式、差角公式需注意的几个问题1.两角和与差的正弦、余弦、正切公式之间的内在联系 (1)掌握好表中公式的内在联系及其推导线索,能帮助学生理解和记忆公式,是学好本部分的关键。(2)诱导公式是两角和、差的三角函数公式的特殊情况。中若有为的整数倍的角时,使用诱导公式更灵活、简便,不需要再用两角和、差公式展开。2.重视角的变换三角变换是三角函数的灵魂与核心,在三角变换中,角的...