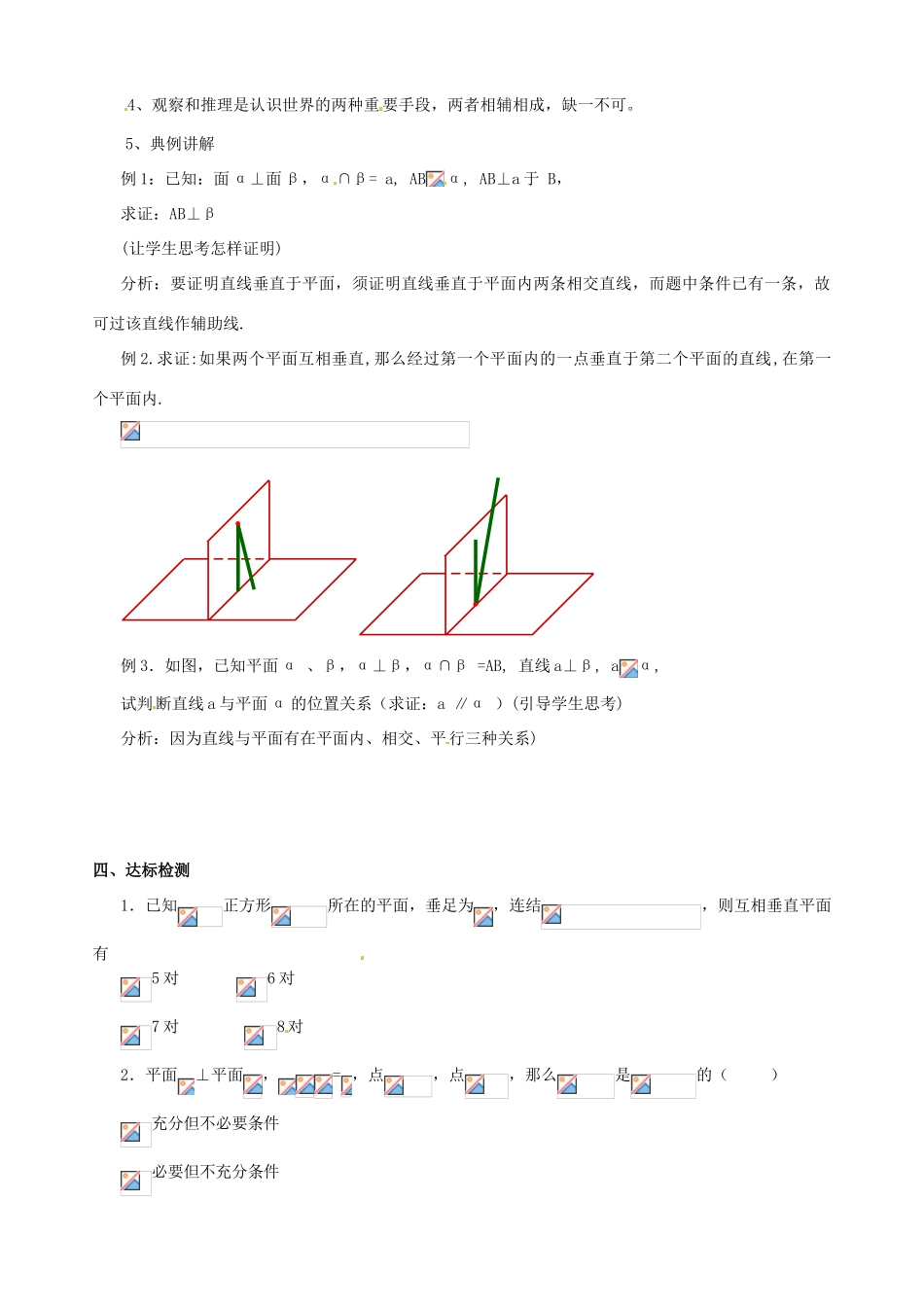
第二章 直线与平面的位置关系学习目标1、知识与技能(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。2、过程与方法利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。3 情态与价值学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。学习重点、难点重点:各知识点间的网络关系;难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。学习过程一、展示目标二、自主学习1、本章知识回顾(1)空间点、线、面间的位置关系;(2)直线、平面平行的判定及性质;(3)直线、平面垂直的判定及性质。2、本章结构框图。三、交流互动1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。公理 1——判定直线是否在平面内的依据;公理 2——提供确定平面最基本的依据;公理 3——判定两个平面交线位置的依据;公理 4——判定空间直线之间平行的依据。2、空间问题解决的重要思想方法:化空间问题为平面问题;3、空间平行、垂直之间的转化与联系:4、观察和推理是认识世界的两种重要手段,两者相辅相成,缺一不可。5、典例讲解例 1:已知:面 α⊥面 β,α∩β= a, ABα, AB⊥a 于 B,求证:AB⊥β(让学生思考怎样证明)分析:要证明直线垂直于平面,须证明直线垂直于平面内两条相交直线,而题中条件已有一条,故可过该直线作辅助线.例 2.求证:如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.例 3.如图,已知平面 α 、β,α⊥β,α∩β =AB, 直线 a⊥β, aα,试判断直线 a 与平面 α 的位置关系(求证:a ∥α )(引导学生思考)分析:因为直线与平面有在平面内、相交、平行三种关系)四、达标检测1.已知正方形所在的平面,垂足为,连结,则互相垂直平面有 5 对 6 对 7 对 8对2.平面⊥平面,= ,点,点,那么是的( ) 充分但不必要条件 必要但不充分条件 充要条件 既不充分也不必要条件3.若三个平面,之间有,,则与 ( )垂直 平行 相交 以上三种可能都有4.已知,是两个平面,直线,,设(1),(2),(3),若以其中两个作为条件,另一个作为结论,则正确命题的个数是 ( )0 1 ...