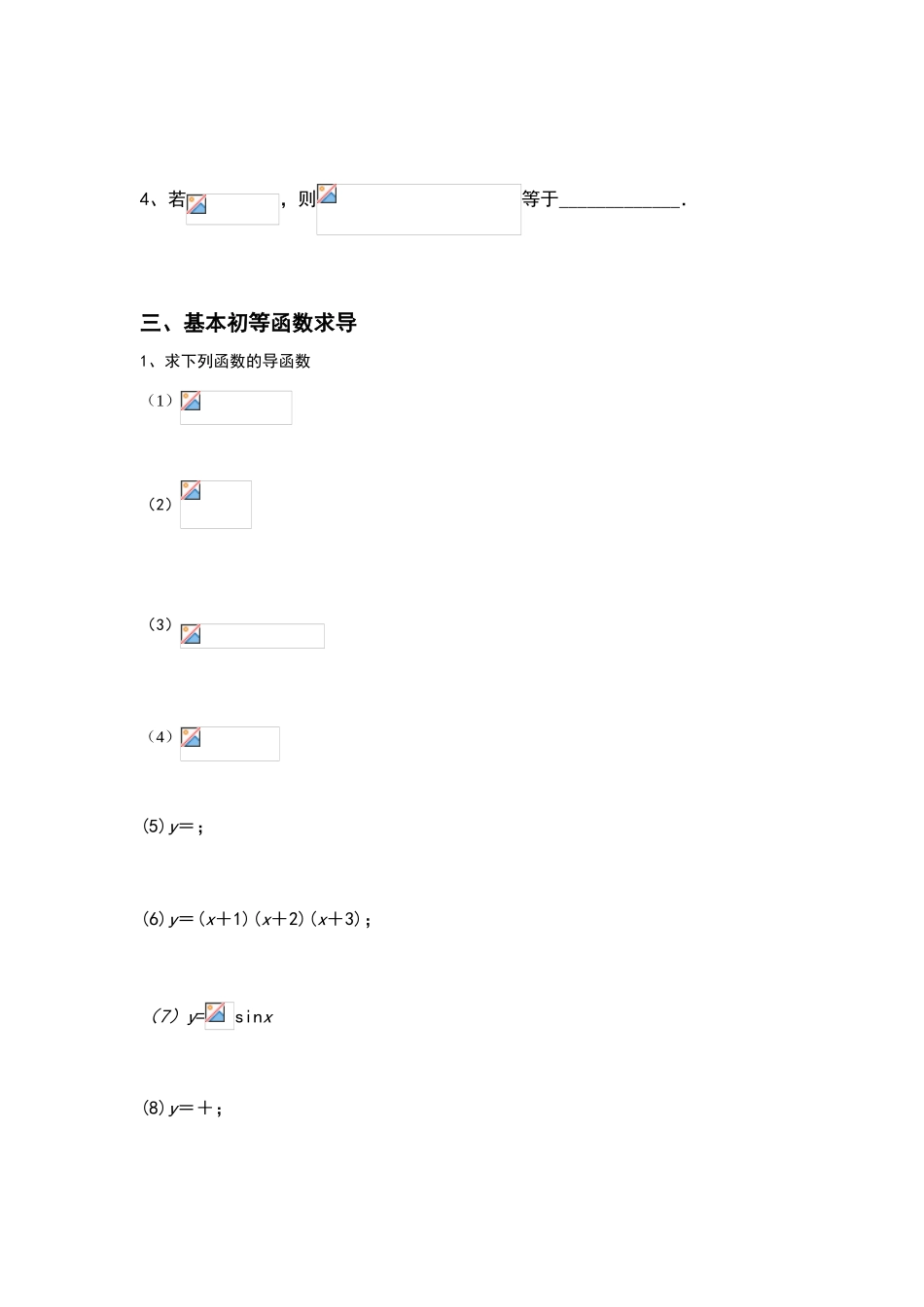
《变化率与导数》(文)一、平均变化率1、已知函数的图象上一点及附近一点,则等于( )A. B. C. D.2、一质点运动的方程为,则在一段时间内相应的平均速度是( )A. B. C. D.二、导数的定义1、设在处可导,则等于( )A. B. C. D.2、若函数在处的切线的斜率为,则极限_______.3、若在处可导,则________________.4、若,则等于_____________.三、基本初等函数求导1、求下列函数的导函数(1) (2) (3) (4) (5)y=;(6)y=(x+1)(x+2)(x+3);(7)y=sinx(8)y=+;(9)y=xnex;(10)y=;(11)y=exln x;(12)y=x2cosx2、若 y=(2x2-3)(x2-4),则 y’= .3、若则 y’= .4、若则 y’= .5、若则 y’= .6、已知 f(x)=,则 f′(x)=___________.7、已知 f(x)=,则 f′(x)=___________.8、已知 f(x)=,则 f′(x)=___________.9.质点运动方程是 s=t2(1+sint),则当 t=时,瞬时速度为___________.10.质点的运动方程是求质点在时刻 t=4 时的速度. 11、f(x)=ax3+3x2+2,若 f′(-1)=4,则 a 的值等于_______12、若 f(x)=x2-2x-4ln x,则 f′(x)>0 的解集为________________13、若函数 f(x)满足 f(x)=x3-f′(1)·x2-x,则 f′(1)的值为( )A.0 B. 2C.1 D.-1四、曲线切线问题1、曲线在处的切线方程是___________2、曲线在点处的切线方程是__________3、函数在处的切线方程是__________________4、与直线 2x-6y+1=0 垂直,且与曲线 y=x3+3x2-1 相切的直线方程是______.5、曲线在点处切线的倾斜角是________6、若曲线的一条切线 与直线垂直,则 的方程是______7、曲线 y=-在点 M 处的切线的斜率为( ).A.- C.- 8、求过点(2,0)且与曲线 y=相切的直线的方程.9、若曲线 f(x)=ax2+lnx 存在垂直于 y 轴的切线,则实数 a 的取值范围是________.10、已知曲线 y=x3+3x2+6x-10 上一点 P,求过曲线上 P 点的所有切线中,斜率最小的切线方程.11、已知函数 f(x)=x3+3xf′(a)(其中 a∈R),且 f(a)=,求:(1)f(x)的表达式;(2)曲线 y=f(x)在 x=a 处的切线方程.12、已知函数 f(x)=x3+x-16.(1)求曲线 y=f(x)在点(2,-6)处的切线的方程;(2)直线 l 为曲线 y=f(x)的切线,且经过原点,求直线 l 的方程及切点坐标;(3)假如曲线 y=f(x)的某一切线与直线 y=-x+3 垂直,求切点坐标与切线的方程...