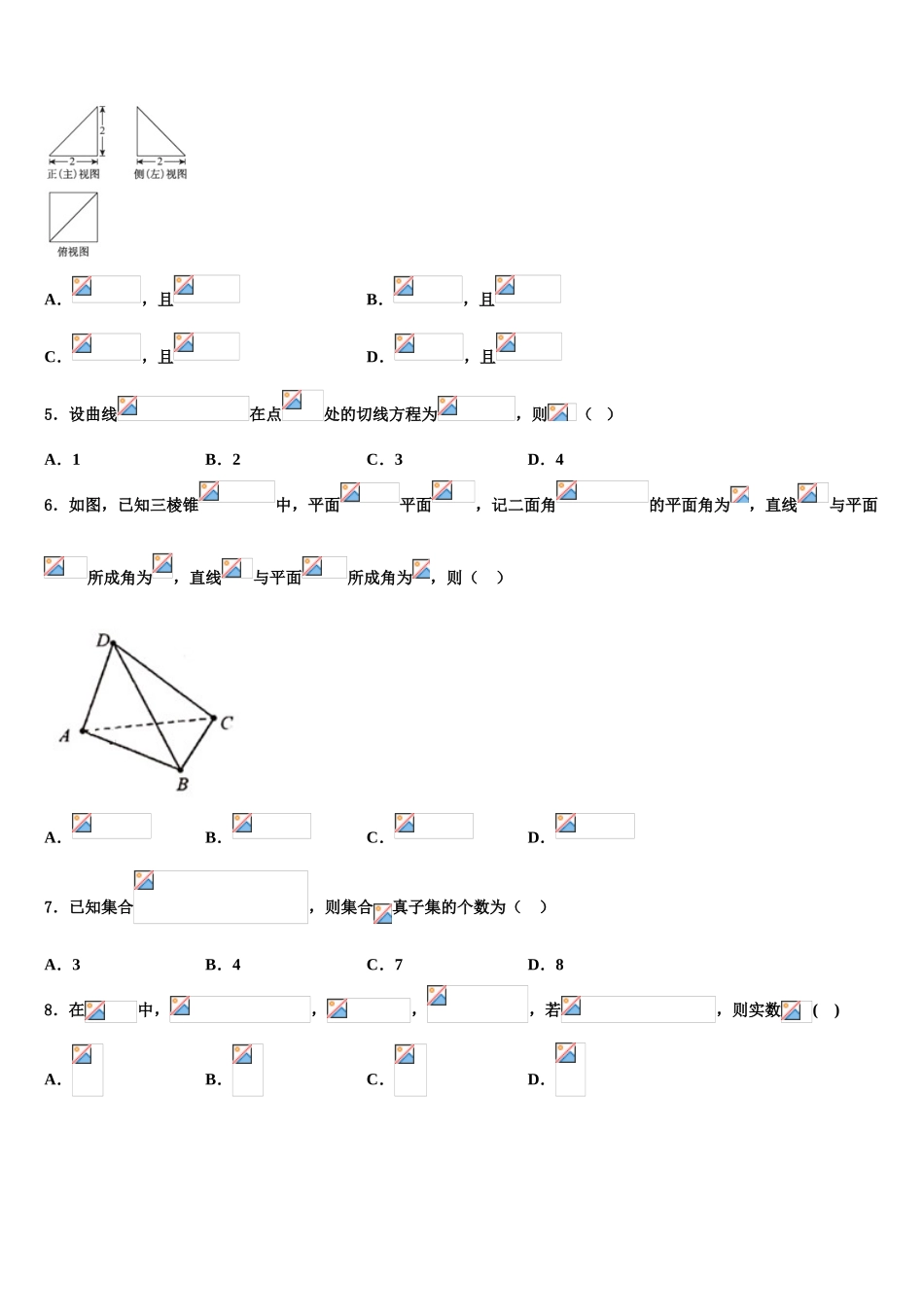
2025-2025 高考数学模拟试卷含解析注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请根据题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数,若关于的不等式恰有 1 个整数解,则实数的最大值为( )A.2B.3C.5D.82.已知,如图是求的近似值的一个程序框图,则图中空白框中应填入A.B.C.D.3.已知集合 A={x|x<1},B={x|},则A.B.C.D.4.某四棱锥的三视图如图所示,记为此棱锥所有棱的长度的集合,则( ).A.,且B.,且C.,且D.,且5.设曲线在点处的切线方程为,则( )A.1B.2C.3D.46.如图,已知三棱锥中,平面平面,记二面角的平面角为,直线与平面所成角为,直线与平面所成角为,则( )A.B.C.D.7.已知集合,则集合真子集的个数为( )A.3B.4C.7D.88.在中,,,,若,则实数( )A.B.C.D.9.点为不等式组所表示的平面区域上的动点,则的取值范围是( )A.B.C.D.10.德国数学家莱布尼兹(1646 年-1716 年)于 1674 年得到了第一个关于 π 的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家 天文学家明安图、(1692 年-1765 年)为提高我国的数学讨论水平,从乾隆初年(1736 年)开始,历时近 30 年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的 6 个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算 π 开创了先河.如图所示的程序框图可以用莱布尼兹“关于 π 的级数展开式”计算 π 的近似值(其中 P 表示 π 的近似值),若输入,则输出的结果是( )A.B.C.D.11.设等比数列的前项和为,若,则的值为( )A.B.C.D.12.已知集合,,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图,直三棱柱中,,,,P 是的中点,则三棱锥的体积为________.14.过且斜率为的直线 交抛物线于两点,为的焦点若的面积等于的面积的 2 倍,则的值为__...