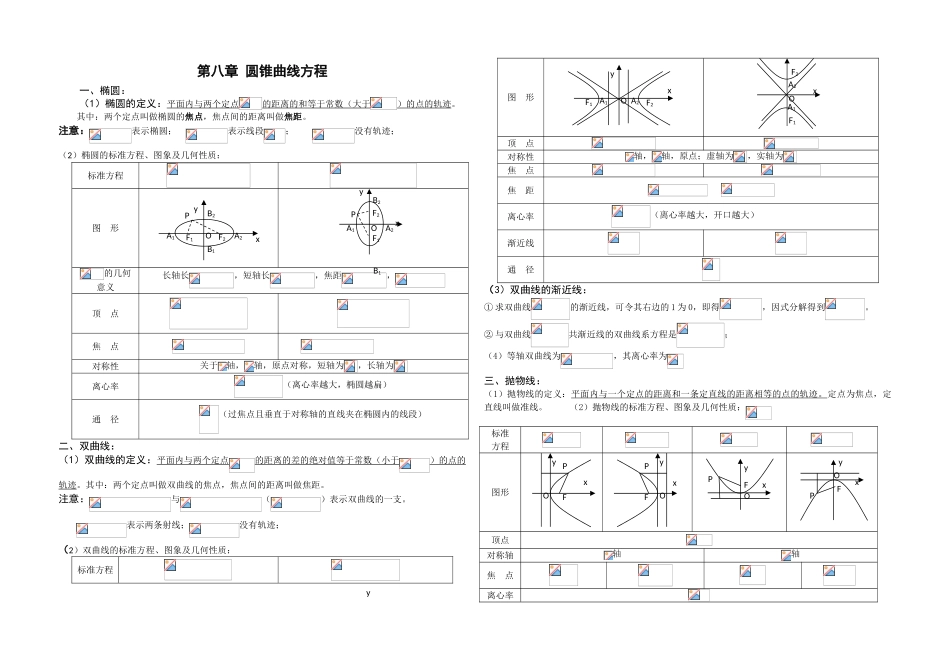
第八章 圆锥曲线方程一、椭圆:(1)椭圆的定义:平面内与两个定点的距离的和等于常数(大于)的点的轨迹。其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距。注意:表示椭圆; 表示线段; 没有轨迹;(2)椭圆的标准方程、图象及几何性质:标准方程图 形的几何意义长轴长,短轴长,焦距,顶 点焦 点对称性关于轴,轴,原点对称,短轴为,长轴为离心率(离心率越大,椭圆越扁)通 径(过焦点且垂直于对称轴的直线夹在椭圆内的线段)二、双曲线:(1)双曲线的定义:平面内与两个定点的距离的差的绝对值等于常数(小于)的点的轨迹。其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距。注意:与()表示双曲线的一支。表示两条射线;没有轨迹;(2)双曲线的标准方程、图象及几何性质:标准方程图 形顶 点对称性轴,轴,原点;虚轴为,实轴为焦 点焦 距 离心率(离心率越大,开口越大)渐近线通 径(3)双曲线的渐近线:① 求双曲线的渐近线,可令其右边的 1 为 0,即得,因式分解得到。② 与双曲线共渐近线的双曲线系方程是;(4)等轴双曲线为,其离心率为三、抛物线:(1)抛物线的定义:平面内与一个定点的距离和一条定直线的距离相等的点的轨迹。定点为焦点,定直线叫做准线。 (2)抛物线的标准方程、图象及几何性质:标准方程图形顶点对称轴轴轴焦 点离心率yB2OF1F2PA2A1B1xA1xOF1F2A2PB2xOF1F2yA2A1xOF1A2A1F2xOFPyOFPyxOFPyxOFPyxyB1y准 线通 径焦半径焦准距训练题一、椭圆1、椭圆上一点 P 到一个焦点的距离为 2,则点 P 到另一个焦点的距离为( )A.5 B. 6 C.7 D.82、已知方程表示椭圆,求的取值范围. 3、已知椭圆的一个焦点坐标为(0,2),求的值为 4、过椭圆的一个焦点,且垂直于轴的直线被此椭圆截得的弦长为( ) A. B. 3 C. D.5、椭圆中,若 CD 为过左焦点的弦,则的周长为( ) A.8 B. 16 C.10 D.与 CD 长有关6、椭圆上一点 M 到焦点的距离为 2,N 为的中心,O 为椭圆中心,则的值是( A.2 B.4 C.8 D. 4、7、椭圆的离心率为,准线方程为,则的椭圆的方程为 8、椭圆上有一点 P,它到左准线的距离为,则 P 到右焦点的距离为 5、9、已知 P 是椭圆上的任意一动点,直线,求点 P 到直线 的距离的最大值和最小值为 10、为何值时,直线和椭圆相交( ) A.或 B. C. 或 D. 11、直线与椭圆总有公共点,则的取值范围是( ) A. B. C.或 D...