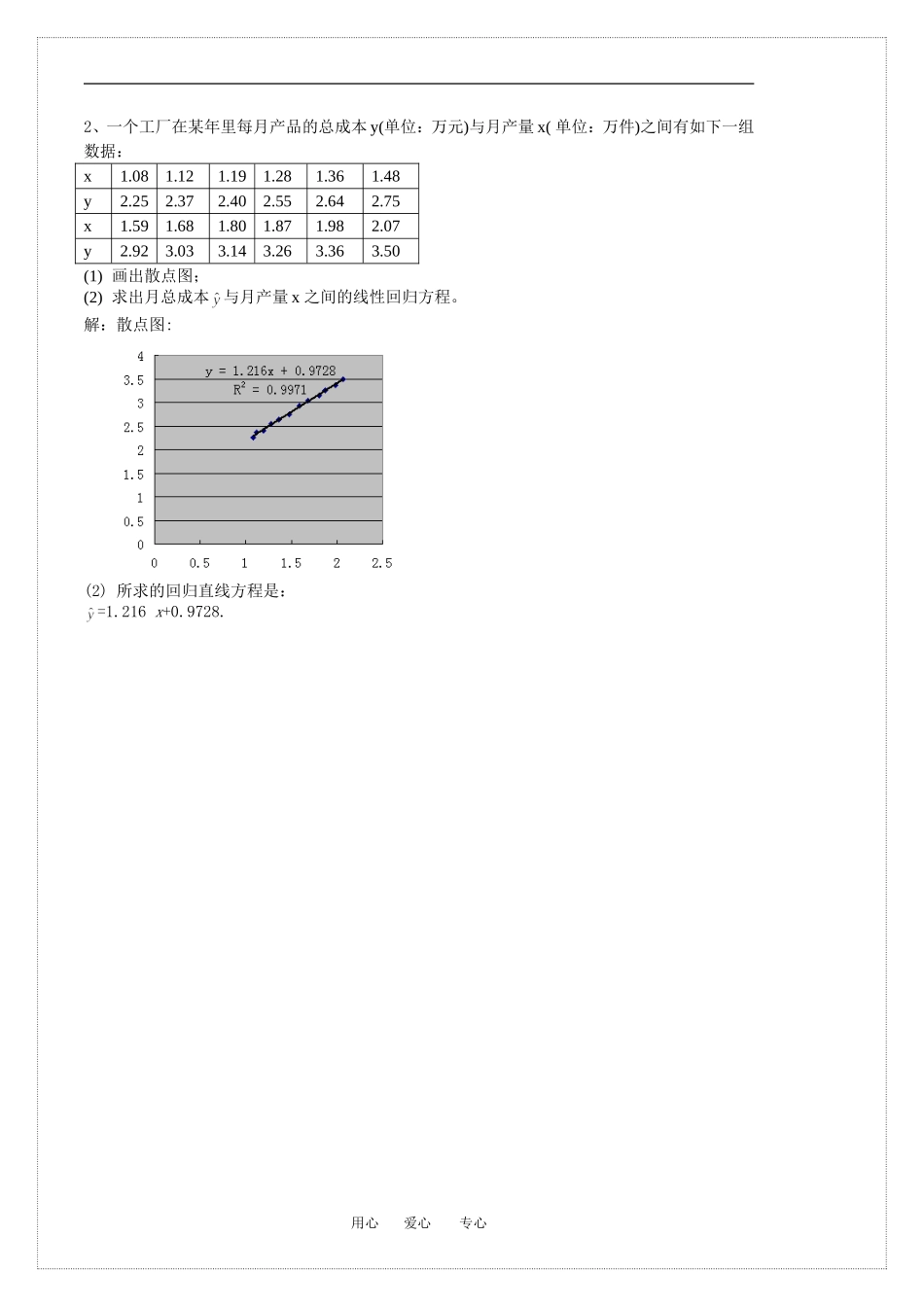
线性回归方程第 26 课时【学习导航】 学习要求 1.进一步了解非确定性关系中两个变量的统计方法;2.进一步掌握回归直线方程的求解方法.【课堂互动】自学评价1.相关关系: 当自变量一定时,因变量的取值带有一定的随机性的两个变量之间的关系 .2.回归分析: 对具有相关关系的两个变量进行统计分析的方法 .3. 求线性回归方程的步骤:(1)xy(2)xyx y(3)iiii计算平均数 、 ,计算与的积,求,计算,,xyii22(4)将上述有关结果代入公式,求,写出回归直线方程.【精典范例】例 1 一个工厂在某年里每月产品的总成本 y(万元)与该月产量 x(万件)之间由如下一组数据:(1)画出散点图;(2)求月总成本 y 与月产量 x 之间的回归直线方程.【解】1)画出散点图: x1y1.41.82.221.61.21.522.533.52)设回归直线方程,用心 爱心 专心x1.081.121.191.281.361.481.591.681.801.871.982.07y2.252.372.402.552.642.752.923.033.143.263.363.50i123456789101112xi1.081.121.191.281.361.481.591.681.801.871.982.07yi2.252.372.402.552.642.752.923.033.143.263.363.50xiyi2.432.2642.8563.2643.5904.074.6435.0905.6526.0966.6537.245=,==2.8475,=29.808,=99.2081,=54.243利用,计算 a,b,得 b≈1.215, a=≈0.974, ∴回归直线方程为:例 2 已知 10 只狗的血球体积及红血球数的测量值如下:454246484235584039506.536.309.527.506.995.909.496.206.598.72(血球体积),(红血球数,百万)(1)画出上表的散点图;(2)求出回归直线度且画出图形.【解】(1)图略(2) =设回归直线方程为,则,= 所以所求回归直线的方程为 追踪训练1、以下是收集到的新房屋销售价格与房屋的大小的数据:房屋大小()80105110115135销售价格(万元)18.42221.624.829.2(1)画出数据的散点图;(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线.【解】(1)散点图(略)(2)所以,线性回归方程为.用心 爱心 专心2、一个工厂在某年里每月产品的总成本 y(单位:万元)与月产量 x( 单位:万件)之间有如下一组数据:x1.081.121.191.281.361.48y2.252.372.402.552.642.75x1.591.681.801.871.982.07y2.923.033.143.263.363.50(1) 画出散点图;(2) 求出月总成本与月产量 x 之间的线性回归方程。解:散点图:(2) 所求的回归直线方程是:=1.216 x+0.9728.用心 爱心 专心