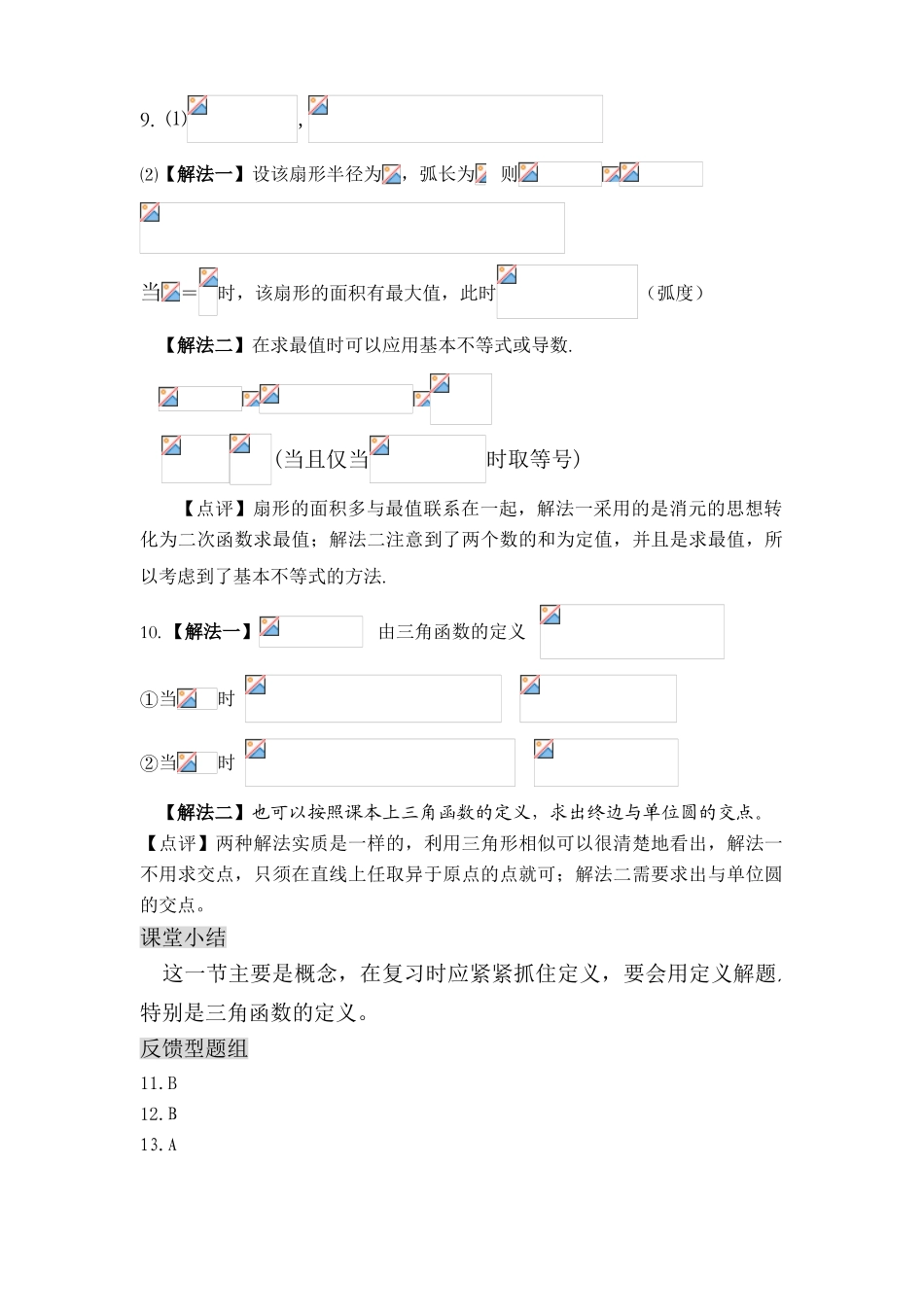
第 6 单元 基本初等函数Ⅱ(三角函数)解答部分§6.1 角的概念推广与任意角的三角函数再现型题组 ⒈ 【提示或答案】B 【基础知识聚焦】角及相关概念的考察⒉ 【提示或答案】C. 【基础知识聚焦】三角函数符号⒊ 【提示或答案】 【基础知识聚焦】三角函数符号4. 【提示或答案】A 【基础知识聚焦】三角函数符号巩固型题组 5.【解法一】分类讨论①角的终边在第二象限 则;②角的终边在第二象限 则.【解法二】也可以按照课本上三角函数的定义,求出终边与单位圆的交点。【点评】两种解法实质是一样的,利用三角形相似可以很清楚地看出,解法一不用求交点,只需在直线上任取异于原点的点就可;解法二需要求出与单位圆的交点。【变式与拓展】已知求角的终边与单位圆的交点的坐标.6. ⑴要使函数有意义 的终边在第一或第二象限,或终边在轴上.⑵要使函数有意义解得:【点评】三角函数的定义域问题同函数的定义与问题一样,需要注意:偶次根式的被开方数,对数的真数,分式的分母等问题,转化出来以后利用三角函数的图象或三角函数线解三角不等式.【变式与拓展】求函数的定义域.7.由 得终边落在第二象限.由 得终边落在第一、二象限及轴正半轴上.【点评】终边相同的角的确定,转化为周期的整数倍.【变式与拓展】如果是第二象限的角,那么的终边落在何处?提高型题组8.⑴角的终边与角的终边相同 令得:在内终边与的终边相同的角为⑵【点评】终边相同的角的集合与终边在过原点的一条直线上的角的集合的表示与运用,从正整数中取出符合条件的值.9. ⑴,⑵【解法一】设该扇形半径为,弧长为 则当=时,该扇形的面积有最大值,此时(弧度)【解法二】在求最值时可以应用基本不等式或导数.(当且仅当时取等号)【点评】扇形的面积多与最值联系在一起,解法一采用的是消元的思想转化为二次函数求最值;解法二注意到了两个数的和为定值,并且是求最值,所以考虑到了基本不等式的方法.10. 【解法一】 由三角函数的定义 ①当时 ②当时 【解法二】也可以按照课本上三角函数的定义,求出终边与单位圆的交点。【点评】两种解法实质是一样的,利用三角形相似可以很清楚地看出,解法一不用求交点,只须在直线上任取异于原点的点就可;解法二需要求出与单位圆的交点。课堂小结 这一节主要是概念,在复习时应紧紧抓住定义,要会用定义解题,特别是三角函数的定义。反馈型题组11.B12.B13.A14.B15.16.令 则 当时有最小值-4又 在时有最小值,有最大值....