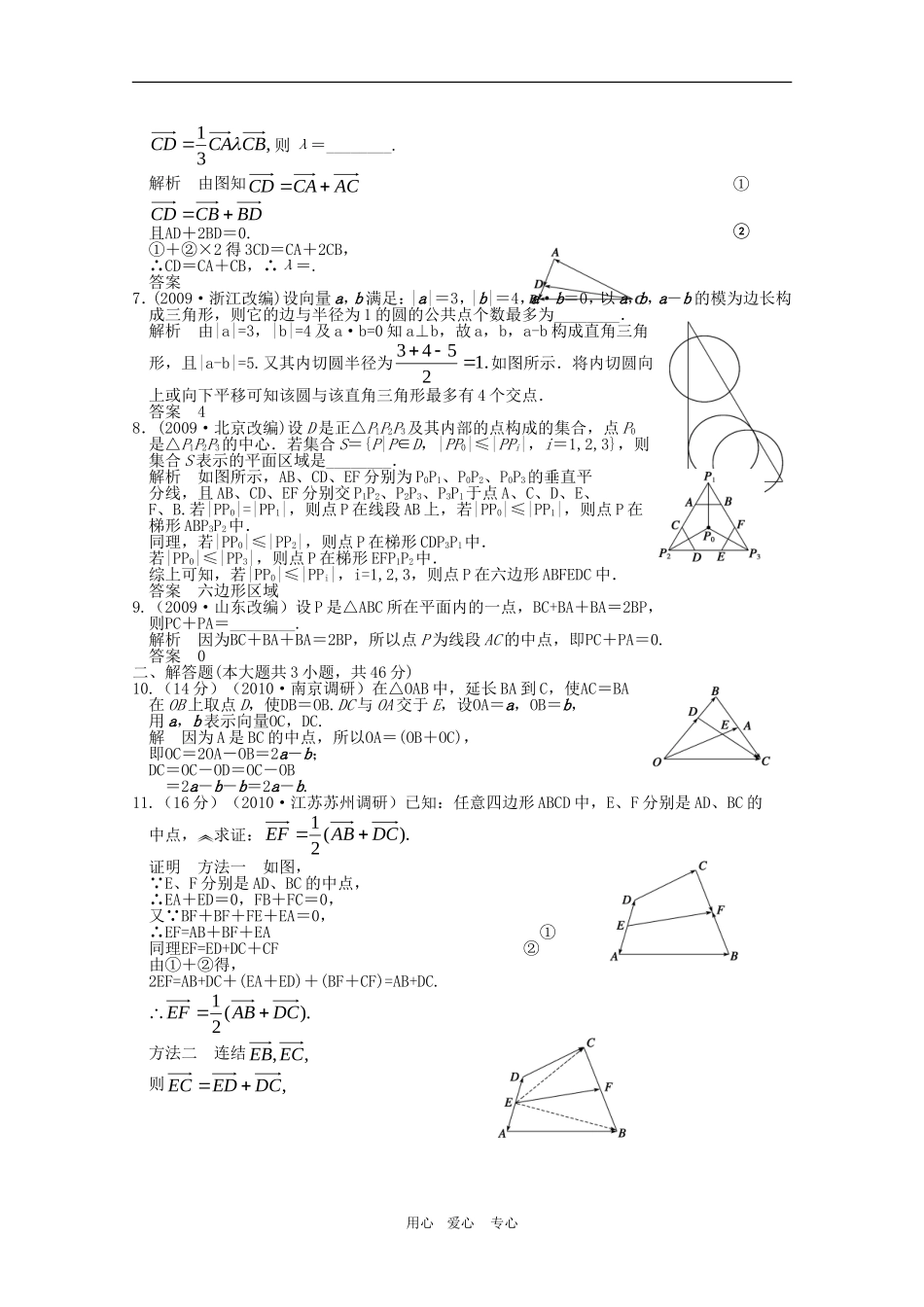
§4.1 平面向量的概念及线性运算一、填空题(本大题共 9 小题,每小题 6 分,共 54 分)1.(2010·苏州模拟)如图所示,在平行四边形 ABCD 中,下列结论中正确的是________.①AB=DC②AD+AB=AC③AB-AD=BD④AD+CB=0解析 ①显然正确;由平行四边形法则知②正确;AB-AD=DB故③不正确;④中AD+CB=AD+DA=0答案 ①②④2.(2010·徐州模拟)设四边形 ABCD 中,有,ABDC21且|,|||BCAD 则这个四边形是 .解析 由AB21DC 知四边形 ABCD 是梯形,又|,|||BCAD 所以四边形 ABCD 是等腰梯形.答案 等腰梯形3.(2008·全国Ⅰ理)在△ABC 中,AB=c,AC=b,若点 D 满足BD=2DC,则AD=____________(用 b,c 表示).解析 如图所示,在△ABC 中,AD=AB+BD.又.32,2BCBDDCBD,cbABACBC∴ABADBC=c+(b-c)=b+c.答案 b+c4.(2010·泰州模拟)如图所示,平面内的两条相交直线 OP1和 OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若,21OPboOPaOP且点 P 落在第Ⅲ部分,则实数 a,b 满足 a______0,b______0(用“>”,“<”或“=”填空).解析 由于点 P 落在第Ⅲ部分,且,21OPboOPaOP则根据实数与向量的积的定义及平行四边形法则知 a>0,b<0.答案 > <5.(2009·江苏南京二模)设OB=xOA+yOC,且 A、B、C 三点共线(该直线不过端点 O),则 x+y=________.解析 A、B、C 三点共线,∴存在一个实数 λ,AB=λAC,即OB-OA=λ(OC-OA).OB=(1-λ)OA+λOC.又 OB=xOA=xOA+yOC,∴x+y=(1-λ)+λ=1.答案 16.(2009·广东茂名一模)在△ABC 中,已知 D 是 AB 边上的一点,若,2DBAD 用心 爱心 专心第四编 平面向量,31CBCACD则 λ=________.解析 由图知ACCACDBDCBCD且AD+2BD=0.①+②×2 得 3CD=CA+2CB,∴CD=CA+CB,∴λ=.答案 7.(2009·浙江改编)设向量 a,b 满足:|a|=3,|b|=4,a·b=0,以 a,b,a-b 的模为边长构成三角形,则它的边与半径为 1 的圆的公共点个数最多为________.解析 由|a|=3,|b|=4 及 a·b=0 知 a⊥b,故 a,b,a-b 构成直角三角形,且|a-b|=5.又其内切圆半径为.12543如图所示.将内切圆向上或向下平移可知该圆与该直角三角形最多有 4 个交点.答案 48.(2009·北京改编)设 D 是正△P1P2P3及其内部的点构成的集合,点 P0是△P1P2P3的中心.若集合 S=...