高二数学辅导资料 圆锥曲线

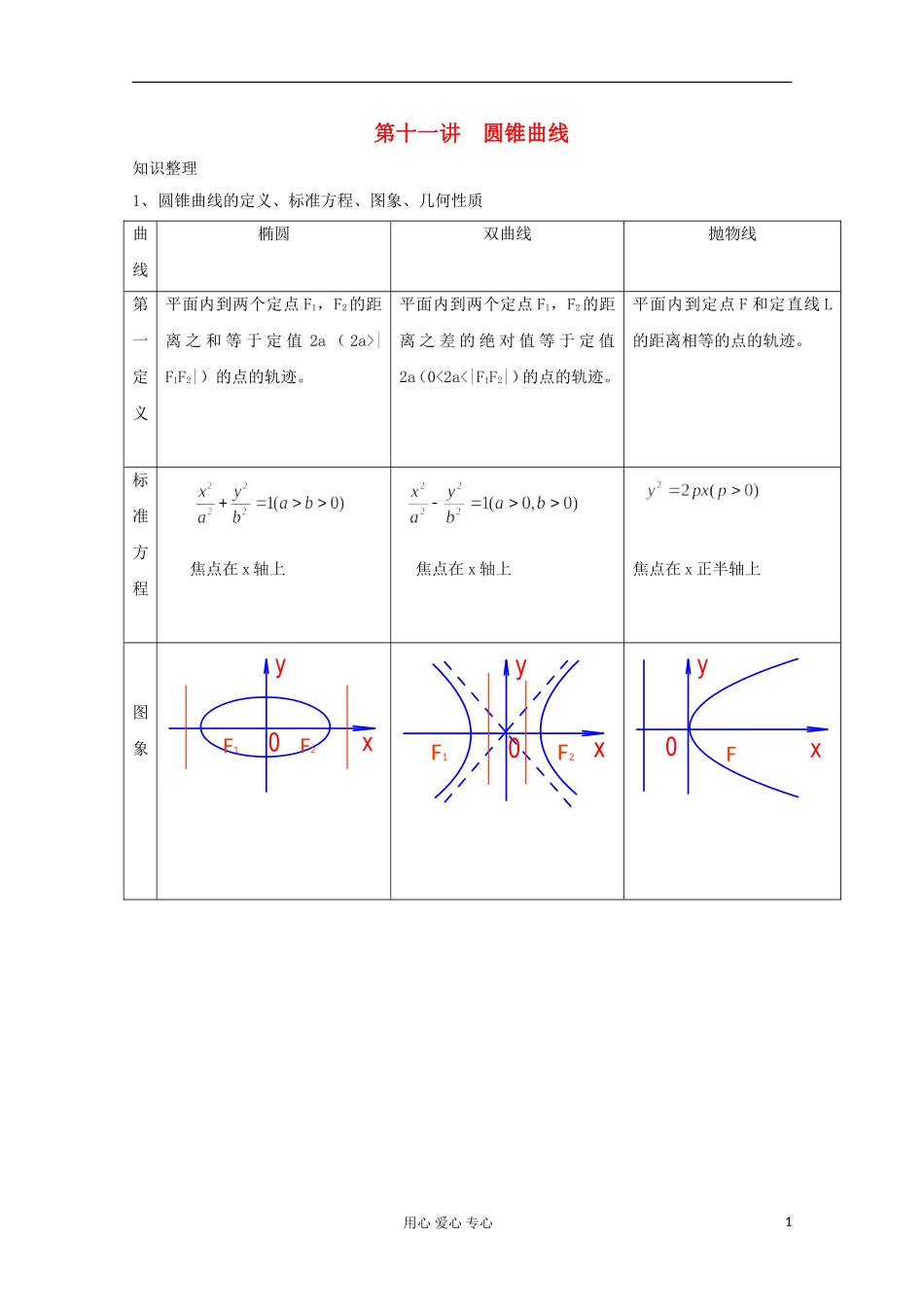
第十一讲 圆锥曲线知识整理1、圆锥曲线的定义、标准方程、图象、几何性质曲线椭圆双曲线抛物线第一定义平面内到两个定点 F1，F2的距离 之 和 等 于 定 值 2a （ 2a>|F1F2|）的点的轨迹。平面内到两个定点 F1，F2的距离 之 差 的 绝 对 值 等 于 定 值2a（0<2a<|F1F2|）的点的轨迹。平面内到定点 F 和定直线 L的距离相等的点的轨迹。标准方程焦点在 x 轴上焦点在 x 轴上焦点在 x 正半轴上图象用心 爱心 专心xy0F1F2xy0F1F2xy0F1圆锥曲线的几何性质渐近线离心率准线对称轴顶点焦点抛物线双曲线椭圆曲线图象),0(),0,(ba)0,(a)0,0(22),0,(bacc22),0,(bacc)0,2( p)1,0(ace),1(ace1exabyx轴，y轴x轴cax22pxxy0Fxy0F1F2xy0F1F2由双曲线求渐进线：由双曲线求渐进线：2、直线和圆锥曲线的位置关系：（1）、判断直线与圆锥曲线的位置关系的方法（基本思路）→消元→一元二次方程→判别式 Δ （方程的思想）（2）、求弦长的方法： ①求交点，利用两点间距离公式求弦长；②弦长公式练习训练1、椭圆 5x2+9y2=45 的离心率是 （ ）用心 爱心 专心2 A.143 B. 2 149 C. 23 D. 322、已知在双曲线的实轴在 y 轴上，它的两条渐近线方程分别是 2x3y=0，实轴长为 12，则它的方程是 （ ） A. xy2236161 B. yx221443241 C. yx2236811 D. yx22122713、以原点为中心，实轴在 x 轴上的双曲线，一条渐近线为 yx34，焦点到渐近线的距离为 6，则它的方程是 （ ） A. xy221691 B. xy229161 C. xy2236641 D. xy22643614、若方程=1 表示双曲线，则其焦距为 ( )(A) (B) 3 (C) 2 (D) 65、方程 y2 = 2px(p>0)中的字母 p 表示 ( ) A．顶点、准线间的距离 B．焦点、准线间的距离 C．原点、焦点间距离 D．以上都不对6、顶点为原点，焦点为 F(0，－1)的抛物线方程是 （ ） A.y2=－2x B.y2=－4x C.x2=－2y D.x2=－4y7、如图，抛物线形拱桥的顶点距水面 2 米时，测得拱桥内水面宽为 12 米，当水面升高 1 米后，拱桥内水面宽度是 ( )(A)6米 (B)6米(C)3米 (D)3米8、（1）已知椭圆的方程为，则它的长轴长为______，短轴长为______，焦距为_____，焦点坐标为________________，离心率为________. （2）已知双曲线的方程为，则它的实轴长为______，虚轴长为_____，焦距为_____，焦点坐标...